题目内容
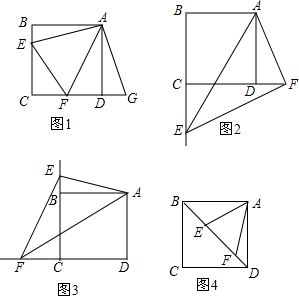
18.如图1,点E,F分别在正方形ABCD的边BC,CD上,∠EAF=45°,连接EF.延长CD至G,使GD=EB,连接AG,易证△AFG≌△AFE.所以EF,BE,DF之间的数量关系为 EF=DF+BE.(1)如图2,点E,F分别在正方形ABCD的边BC,CD的延长线上,∠EAF=45°,连接EF.试猜想EF,BE,DF之间的数量关系;(直接写出结果,不需证明)
(2)如图3,点E,F分别在正方形ABCD的边CB,DC的延长线上,∠EAF=45°,连接EF.试猜想EF,BE,DF之间的数量关系,并加以证明;
(3)如图4,点E,F在正方形ABCD的对角线BD上,∠EAF=45°,若BE=2,DF=1,请直接写出EF的长.
分析 (1)在BE上截取BG=DF,连接AG;先由SAS证明△ABG≌△ADF,得出AG=AF,∠BAG=∠DAF,再证出∠EAG=∠EAF,由SAS证明△AEG≌△AEF,得出EG=EF,即可得出结论;(2)在CD上截取DG=BE,连接AG;先由SAS证明△ABE≌△ADG,得出∠EAB=∠GAD,AE=AG,再证出∠GAF=∠EAF,由SAS证明△AEF≌△AGF,得出EF=GF,即可得出结论;
(3)作BM⊥BD,并在BM上截取BG=DF=1,连接AG、EG;先由勾股定理求出EG,求出∠ABG=∠ADF,由SAS证明△ABG≌△ADF,得出AG=AF,∠BAG=∠DAF,证出∠EAG=∠EAF,证明△AEG≌△AEF,得出EF=EG即可.
解答 (1)解:BE=DF+EF;理由如下:
在BE上截取BG=DF,连接AG;如图2所示: ∵四边形ABCD是正方形,
∵四边形ABCD是正方形,
∴AB=BC=AD,∠BAD=∠B=∠ADC=∠ADF=90°,
在△ABG和△ADF中,$\left\{\begin{array}{l}{AB=AD}\\{∠B=∠ADF}\\{BG=DF}\end{array}\right.$,
∴△ABG≌△ADF(SAS),
∴AG=AF,∠BAG=∠DAF,
∴∠GAF=90°,
∵∠EAF=45°,
∴∠EAG=45°,
∴∠EAG=∠EAF,
在△AEG和△AEF中,$\left\{\begin{array}{l}{AG=AF}\\{∠EAG=∠EAF}\\{AE=AE}\end{array}\right.$,
∴△AEG≌△AEF(SAS),
∴EG=EF,
∴EG+BG=EF+DF,
即BE=EF+DF;
(2)解:DF=EF+BE;理由如下:
在CD上截取DG=BE,连接AG;如图3所示:
∵四边形ABCD是正方形,
∴AB=AD,∠BAD=∠D=∠ABC=∠ABE=90°,
在△ABE和△ADG
中,$\left\{\begin{array}{l}{BE=DG}\\{∠ABE=∠D}\\{AB=AD}\end{array}\right.$,∴△ABE≌△ADG(SAS),
∴∠EAB=∠GAD,AE=AG,
∴∠EAG=90°,
∵∠EAF=45°,
∴∠GAF=45°,
∴∠GAF=∠EAF,在△AEF和△AGF中,$\left\{\begin{array}{l}{AE=AG}\\{∠EAF=∠GAF}\\{AF=AF}\end{array}\right.$,
∴△AEF≌△AGF(SAS),
∴EF=GF,
∵DF=GF+GD,
∴DF=EF+BE;
(3)解:EF的长为$\sqrt{5}$,理由如下:
作BM⊥BD,并在BM上截取BG=DF=1,连接AG、EG;如图4所示:
则∠EBG=90°,
∴EG=$\sqrt{B{E}^{2}+B{G}^{2}}$=$\sqrt{{2}^{2}+{1}^{2}}$=$\sqrt{5}$,
∵四边形ABCD是正方形,
∴AB=AD,∠BAD=∠ABC=∠ADC=90°,∠ABD=∠ADF=45°,
∴∠ABG=45°,
∴∠ABG=∠ADF,
在△ABG和△ADF中,$\left\{\begin{array}{l}{BG=DF}&{\;}\\{∠ABG=∠ADF}&{\;}\\{AB=AD}&{\;}\end{array}\right.$,
∴△ABG≌△ADF(SAS),
∴AG=AF,∠BAG=∠DAF,
∴∠GAF=90°,
∵∠EAF=45°,
∴∠EAG=45°,
∴∠EAG=∠EAF,
在△AEG和△AEF中,$\left\{\begin{array}{l}{AG=AF}&{\;}\\{∠EAG=∠EAF}&{\;}\\{AE=AE}&{\;}\end{array}\right.$,
∴△AEG≌△AEF(SAS),
∴EG=EF,
∴EF=$\sqrt{5}$.
点评 本题是四边形综合题目,考查了正方形的性质、全等三角形的判定与性质、勾股定理等知识;本题难度较大,综合性强;每小题都需要通过作辅助线证明两次三角形全等才能得出结论.

 一卷搞定系列答案
一卷搞定系列答案 名校作业本系列答案
名校作业本系列答案 轻巧夺冠周测月考直通名校系列答案
轻巧夺冠周测月考直通名校系列答案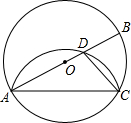 在⊙O中,AB为直径,点C为圆上一点,将劣弧$\widehat{AC}$沿弦AC翻折交AB于点D,连结CD.如图,若点D与圆心O不重合,∠BAC=25°,则∠DCA的度数( )
在⊙O中,AB为直径,点C为圆上一点,将劣弧$\widehat{AC}$沿弦AC翻折交AB于点D,连结CD.如图,若点D与圆心O不重合,∠BAC=25°,则∠DCA的度数( )| A. | 35° | B. | 40° | C. | 45° | D. | 65° |
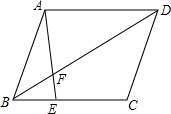 如图,在?ABCD中,E为BC边上的点,若BE:EC=4:5,AE交BD于F,则BF:FD等于( )
如图,在?ABCD中,E为BC边上的点,若BE:EC=4:5,AE交BD于F,则BF:FD等于( )| A. | 4:5 | B. | 3:5 | C. | 4:9 | D. | 3:8 |
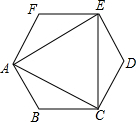 顺次连接正六边形的三个不相邻的顶点,得到如图的图形,下列说法错误的是( )
顺次连接正六边形的三个不相邻的顶点,得到如图的图形,下列说法错误的是( )| A. | △ACE是等边三角形 | B. | 既是轴对称图形也是中心对称图形 | ||
| C. | 连接AD,则AD分别平分∠EAC与∠EDC | D. | 图中一共能画出3条对称轴 |
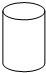 如图是一个圆柱体,则它的主视图是( )
如图是一个圆柱体,则它的主视图是( )| A. |  | B. |  | C. |  | D. | 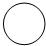 |
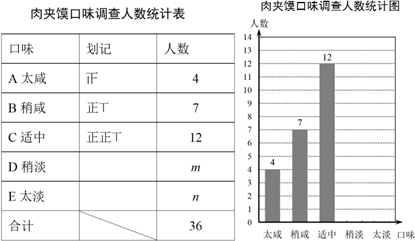
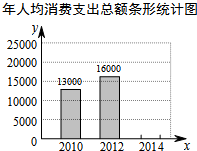 随着生活质量的提高,人们的消费水平逐年上升,小明把自己家2010,2012,2014年的消费数据绘制统计图表如下:
随着生活质量的提高,人们的消费水平逐年上升,小明把自己家2010,2012,2014年的消费数据绘制统计图表如下:年人均各项消费支出统计表
| 年份 支出项目(单位:元) | 2010年 | 2012年 | 2014年 |
| 食品支出 | a | 5600 | 6300 |
| 医疗、保健支出 | 2000 | 2200 | 3000 |
| 家庭用品及服务支出 | 3300 | 4000 | 5700 |
| 其他支出 | 2500 | 4200 | 6000 |
(1)a=5200;并补全条形统计图;
(2)我们把“食品支出总额占个人消费支出总额的百分数”叫做恩格尔系数,请分别求出小明家2010,2012,2014年的恩格尔系数,并根据变化情况谈谈你的看法.
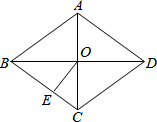 如图,菱形ABCD的面积为S,对角线交于点O,OE⊥BC于点E.下列结论正确的是( )
如图,菱形ABCD的面积为S,对角线交于点O,OE⊥BC于点E.下列结论正确的是( )| A. | S=AC•BD | B. | S=4BC•OE | C. | S=2AB•OE | D. | S=2BD•AO |

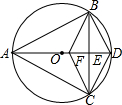 如图,已知△ABC内接于⊙O,且AB=AC,直径AD交BC于点E,F是OE上的一点,使CF∥BD.
如图,已知△ABC内接于⊙O,且AB=AC,直径AD交BC于点E,F是OE上的一点,使CF∥BD.