题目内容
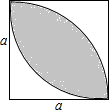 一块正方形苗圃的造型如图所示(单位:m),它的阴影部分和空白部分将分成两种颜色的花地.根据所给的数据,求图中阴影部分的面积和空白部分的面积各是多少?
一块正方形苗圃的造型如图所示(单位:m),它的阴影部分和空白部分将分成两种颜色的花地.根据所给的数据,求图中阴影部分的面积和空白部分的面积各是多少?考点:列代数式
专题:
分析:先计算正方形的面积为:a2,扇形的面积
πa2,然后用正方形的面积减去扇形的面积即可得到一个空白部分的面积:a2-
πa2,所以两个空白部分的面积:2a2-
πa2,然后再用正方形的面积减去两个空白部分的面积即可得到阴影部分的面积:
πa2-a2.
| 1 |
| 4 |
| 1 |
| 4 |
| 1 |
| 2 |
| 1 |
| 2 |
解答:解:∵正方形的面积为:a2,扇形的面积
πa2,
∴空白部分的面积:2(a2-
πa2)=2a2-
πa2,
∵阴影部分的面积=正方形的面积-空白部分的面积
∴阴影部分的面积:a2-(2a2-
πa2)=
πa2-a2.
所以图中阴影部分的面积和空白部分的面积各是
πa2-a2、2a2-
πa2.
| 1 |
| 4 |
∴空白部分的面积:2(a2-
| 1 |
| 4 |
| 1 |
| 2 |
∵阴影部分的面积=正方形的面积-空白部分的面积
∴阴影部分的面积:a2-(2a2-
| 1 |
| 2 |
| 1 |
| 2 |
所以图中阴影部分的面积和空白部分的面积各是
| 1 |
| 2 |
| 1 |
| 2 |
点评:此题考查了列代数式,解题的关键是:明确空白部分的面积和阴影部分的面积如何表示.

练习册系列答案
相关题目
某次知识竞赛共有20道题,每一题答对得10分,答错或不答都扣5分,娜娜得分要超过90分,则她至少要答对( )
| A、10道题 | B、12道题 |
| C、13道题 | D、16道题 |
 如图,在△ABC中,∠ABC=90°,点D是AB上一点,且DB=BC,DE平行BC,点P为AC边上的点,DB=DP.
如图,在△ABC中,∠ABC=90°,点D是AB上一点,且DB=BC,DE平行BC,点P为AC边上的点,DB=DP. 已知△ABC和△EDC都是等边三角形,将∠CDE绕C点旋转.
已知△ABC和△EDC都是等边三角形,将∠CDE绕C点旋转. 画出如图立体图形的三视图.
画出如图立体图形的三视图.