题目内容
5. 如图,AD∥BC,∠D=90°,DC=7,AD=2,BC=4,若在边DC上有点P使△PAD和△PBC相似,则这样的点P点呢?若存在求出DP的值.
如图,AD∥BC,∠D=90°,DC=7,AD=2,BC=4,若在边DC上有点P使△PAD和△PBC相似,则这样的点P点呢?若存在求出DP的值.
分析 设DP=x,表示出CP=7-x,然后分①AD和BC是对应边,②AD和CP是对应边两种情况,利用相似三角形对应边成比例列式计算即可得解.
解答 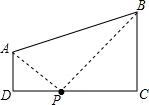 解:存在;理由如下:
解:存在;理由如下:
如图所示:设DP=x,则CP=7-x,
①AD和BC是对应边时,△ADP∽△BCP,
∴$\frac{AD}{BC}=\frac{DP}{CP}$,
即$\frac{2}{4}=\frac{x}{7-x}$,
解得:x=$\frac{7}{3}$;
②AD和CP是对应边时,△ADP∽△PCB,
∴$\frac{AD}{CP}=\frac{DP}{BC}$,
即$\frac{2}{7-x}=\frac{x}{4}$,
整理得:x2-7x+8=0,
解得:x=$\frac{7±\sqrt{17}}{2}$;
综上所述,当DP=$\frac{7}{3}$或=$\frac{7±\sqrt{17}}{2}$时,△PAD和△PBC相似.
点评 本题考查了相似三角形的判定,一元二次方程的解法,难点在于分情况讨论.

练习册系列答案
 英才计划同步课时高效训练系列答案
英才计划同步课时高效训练系列答案
相关题目
20.用边长为4cm,5cm,6cm的两个全等三角形拼成四边形,一共能拼成( )个平行四边形.
| A. | 4 | B. | 3 | C. | 2 | D. | 1 |
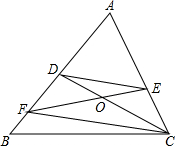 如图,在△ABC中,∠ACD=∠B,将△ACD绕A点旋转,点D落在点E处,点C落在点F处,CD,EF交于O点,连接DE,FC,找出其中相似三角形.
如图,在△ABC中,∠ACD=∠B,将△ACD绕A点旋转,点D落在点E处,点C落在点F处,CD,EF交于O点,连接DE,FC,找出其中相似三角形.
 如图:计算下面各个图形的表面积与体积.
如图:计算下面各个图形的表面积与体积. 如图,拦水坝的横断面为梯形ABCD,坝高23米.坝面宽BC=6米.根据条件求:
如图,拦水坝的横断面为梯形ABCD,坝高23米.坝面宽BC=6米.根据条件求: 如图所示,已知等边三角形ABC的外接圆⊙O的半径为R,求△ABC的边长a、周长P、边心距r及面积S.
如图所示,已知等边三角形ABC的外接圆⊙O的半径为R,求△ABC的边长a、周长P、边心距r及面积S. 下面是由五块积木搭成的一个几何体,这五块积木都是棱长为1的正方体.
下面是由五块积木搭成的一个几何体,这五块积木都是棱长为1的正方体. 分别画出图中几何体的主视图,左视图和俯视图.
分别画出图中几何体的主视图,左视图和俯视图.