题目内容
13.已知:a=$\frac{1}{2-\sqrt{3}}$,b=$\frac{1}{2+\sqrt{3}}$,求a2+3ab+b2的值.分析 根据分母有理化法则化简a、b,根据完全平方公式把所求的代数式变形,代入计算即可.
解答 解:a=$\frac{1}{2-\sqrt{3}}$=2+$\sqrt{3}$,b=$\frac{1}{2+\sqrt{3}}$2-$\sqrt{3}$,
则a+b=4,ab=1,
a2+3ab+b2=(a+b)2+ab=17.
点评 本题考查的是二次根式的计算,掌握分母有理化法则、平方差公式和完全平方公式是解题的关键.

练习册系列答案
 巧学巧练系列答案
巧学巧练系列答案
相关题目
4.当x是怎样的实数时,$\sqrt{x-2}$在实数范围内有意义?( )
| A. | x≥3 | B. | x≥2 | C. | x≥1 | D. | x≥4 |
1.下列事件是随机事件的是( )
| A. | 在一个仅装着白球和黑球的袋中摸球,摸出红球 | |
| B. | 在一个标准大气压下,加热到100℃,水沸腾 | |
| C. | 有一名运动员奔跑的速度是30米/秒 | |
| D. | 购买一张福利彩票,中奖 |
8.为了解某小区家庭垃圾袋的使用情况,小亮随机调查了该小区 10 户家庭一周的使用数量,结果如下(单位:个):7,9,11,8,7,14,10,8,9,7.关于这组数据,下列结论错误的是( )
| A. | 极差是 7 | B. | 众数是 8 | C. | 中位数是 8.5 | D. | 平均数是 9 |
 如图,已知∠ADE=70°,DF平分∠ADE,∠2=35°,求证:DF∥BE.
如图,已知∠ADE=70°,DF平分∠ADE,∠2=35°,求证:DF∥BE.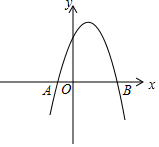 如图,在平面直角坐标系xOy中,已知抛物线y=-x2+2x+3与x轴交于A,B两点,点M在这条抛物线上,点P在y轴上,如果以点P、M、A、B为顶点的四边形是平行四边形,求点M的坐标.
如图,在平面直角坐标系xOy中,已知抛物线y=-x2+2x+3与x轴交于A,B两点,点M在这条抛物线上,点P在y轴上,如果以点P、M、A、B为顶点的四边形是平行四边形,求点M的坐标.
 如图,已知△ABC(AC<BC),用尺规在BC上确定一点P,使PA+PC=BC.
如图,已知△ABC(AC<BC),用尺规在BC上确定一点P,使PA+PC=BC.