题目内容
20．
图象中所反映的过程是：张军从家跑步去体育场，在那里锻炼了一阵后，又去早餐店吃早餐，然后散步走回家，其中x表示时间，y表示张强离家的距离，根据图象提供的信息，以下四个说法中错误的是（ ）| A． | 体育场离早餐店4千米 | |
| B． | 张军在体育场锻炼了0.25小时 | |
| C． | 体育场离张强家2.5千米 | |
| D． | 张军从早餐店回家的平均速度是$\frac{18}{7}$千米/小时 |
分析 根据图象，结合语言叙述，逐项分析计算得出答案即可．
解答 解：A、因为体育场离张强家2.5千米，而早餐店离家越来越近，所以体育场离早餐店4千米错误，符合题意；
B、张军在体育场锻炼了30-15=15分钟=0.25小时，此选项不合题意；
C、体育场离张强家2.5千米，此选项不合题意；
D、从图象可知：文具店离张强家1.5千米，张强从文具店散步走回家花了100-65=35分，
所以张强从文具店回家的平均速度是$\frac{1.5}{35}$×60=$\frac{18}{7}$千米/小时，此选项不合题意．
故选：A．
点评 本题考查利用函数的图象解决实际问题，正确理解函数图象横纵坐标表示的意义，理解问题的过程，就能够通过图象得到函数问题的相应解决．
练习册系列答案
培优三好生系列答案
优化作业上海科技文献出版社系列答案
相关题目
11．下列各组数是勾股数的是（ ）
| A． | 3，4，5 | B． | 7，8，9 | C． | 9，41，47 | D． | 52，122，132 |
15．把多项式4a3-8a2b+4ab2分解因式，结果正确的是（ ）
| A． | a（2a+b）（a-2b） | B． | 4a（a2-2ab+b2） | C． | a（2a-b）2 | D． | 4a（a-b）2 |
如图，△ABC中，∠C=90°，CD=15cm，BD=25cm，AC=30cm，求证：∠1=∠2．
如图，在平面直角坐标系中，直线AB与x轴、y轴的正半轴分别交于点A，B，直线CD与x轴正半轴、y轴负半轴分别交于点D，C，AB与CD相交于点E，点A，B，C，D的坐标分别为（8，0）、（0，6）、（0，-3）、（4，0），点M是OB的中点，点P在直线AB上，过点P作PQ∥y轴，交直线CD于点Q，设点P的横坐标为m．
10．
问题：我们已经知道反比例函数的图象是双曲线，那么函数y=$\frac{6}{|x|-3}$的图象是怎样的呢？
经验：
（1）我们在研究反比例函数的图象和性质的时候是从以下两个方面来探究的：
①由数想到形----先根据表达式中x、y的数量关系，初步估计图象的基本概貌．如：形状（直线或曲线）；位置（所在区域、与直线或坐标轴的交点情况）；趋势（上升、下降）；对称性等．
②描点画图----根据已有的函数画图的经验，利用描点画图．
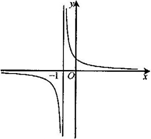
（2）我们知道，函数y=$\frac{2}{x+1}$的图象是如图所示的两条曲线，一支在过点（-1，0）且平行于y轴的直线的右侧且在x轴的上方，另一支在过点（-1，0）且平行于y轴的直线的左侧且在x轴的下方．
探索：请你根据以上经验，研究函数y=$\frac{6}{|x|-3}$的图象和性质并解决相关问题．
（1）由数想形：
（2）描点画图：
①列表：
②画图：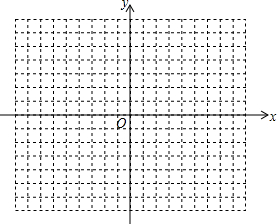
应用：观察你所画的函数图象，解答下列问题：
（3）若点A（a，c），B（b，c）为该函数图象上不同的两点，则a+b=0；
（4）直接写出当$\frac{6}{|x|-3}$≥-2时x的取值范围．
问题：我们已经知道反比例函数的图象是双曲线，那么函数y=$\frac{6}{|x|-3}$的图象是怎样的呢？经验：
（1）我们在研究反比例函数的图象和性质的时候是从以下两个方面来探究的：
①由数想到形----先根据表达式中x、y的数量关系，初步估计图象的基本概貌．如：形状（直线或曲线）；位置（所在区域、与直线或坐标轴的交点情况）；趋势（上升、下降）；对称性等．
②描点画图----根据已有的函数画图的经验，利用描点画图．
（2）我们知道，函数y=$\frac{2}{x+1}$的图象是如图所示的两条曲线，一支在过点（-1，0）且平行于y轴的直线的右侧且在x轴的上方，另一支在过点（-1，0）且平行于y轴的直线的左侧且在x轴的下方．
探索：请你根据以上经验，研究函数y=$\frac{6}{|x|-3}$的图象和性质并解决相关问题．
（1）由数想形：
（2）描点画图：
①列表：
| x | … | … | |||||||||||||||
| y | … | … |
应用：观察你所画的函数图象，解答下列问题：
（3）若点A（a，c），B（b，c）为该函数图象上不同的两点，则a+b=0；
（4）直接写出当$\frac{6}{|x|-3}$≥-2时x的取值范围．