题目内容
5.已知:A=($\frac{x}{x-1}$-$\frac{x}{{x}^{2}-1}$)÷$\frac{{x}^{2}-x}{{x}^{2}-2x+1}$(1)化简A;
(2)当x是满足不等式组$\left\{\begin{array}{l}{2x+5≥3}\\{\frac{1-3x}{2}>-4}\end{array}\right.$的整数时,求A的值.
分析 (1)原式括号中两项通分并利用同分母分式的减法法则计算,同时利用除法法则变形,约分即可得到结果;
(2)求出不等式组的解集确定出整数解得到x的值,代入(1)中结果计算即可得到结果.
解答 解:(1)A=$\frac{x(x+1)-x}{(x+1)(x-1)}$•$\frac{(x-1)^{2}}{x(x-1)}$=$\frac{{x}^{2}}{(x+1)(x-1)}$•$\frac{x-1}{x}$=$\frac{x}{x+1}$;
(2)$\left\{\begin{array}{l}{2x+5≥3①}\\{\frac{1-3x}{2}>-4②}\end{array}\right.$,
由①得:x≥-1,
由②得:x<3,
∴不等式组的解集为-1≤x<3,即整数解为-1,0,1,2,
当x=-1,0,1时,原式没有意义;
则当x=2时,原式=$\frac{2}{3}$.
点评 此题考查了分式的混合运算,以及一元一次不等式组的整数解,熟练掌握运算法则是解本题的关键.

练习册系列答案
相关题目
13.若一组数据1,2,4,5,6,x中,有唯一的众数是1,这组数据的中位数是( )
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
20. 图象中所反映的过程是:张军从家跑步去体育场,在那里锻炼了一阵后,又去早餐店吃早餐,然后散步走回家,其中x表示时间,y表示张强离家的距离,根据图象提供的信息,以下四个说法中错误的是( )
图象中所反映的过程是:张军从家跑步去体育场,在那里锻炼了一阵后,又去早餐店吃早餐,然后散步走回家,其中x表示时间,y表示张强离家的距离,根据图象提供的信息,以下四个说法中错误的是( )
 图象中所反映的过程是:张军从家跑步去体育场,在那里锻炼了一阵后,又去早餐店吃早餐,然后散步走回家,其中x表示时间,y表示张强离家的距离,根据图象提供的信息,以下四个说法中错误的是( )
图象中所反映的过程是:张军从家跑步去体育场,在那里锻炼了一阵后,又去早餐店吃早餐,然后散步走回家,其中x表示时间,y表示张强离家的距离,根据图象提供的信息,以下四个说法中错误的是( )| A. | 体育场离早餐店4千米 | |
| B. | 张军在体育场锻炼了0.25小时 | |
| C. | 体育场离张强家2.5千米 | |
| D. | 张军从早餐店回家的平均速度是$\frac{18}{7}$千米/小时 |
17.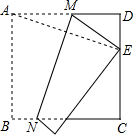 如图,将边长为12cm的正方形ABCD折叠,使得点A落在CD边上的点E处,折痕为MN.若CE的长为7cm,则MN的长为( )
如图,将边长为12cm的正方形ABCD折叠,使得点A落在CD边上的点E处,折痕为MN.若CE的长为7cm,则MN的长为( )
 如图,将边长为12cm的正方形ABCD折叠,使得点A落在CD边上的点E处,折痕为MN.若CE的长为7cm,则MN的长为( )
如图,将边长为12cm的正方形ABCD折叠,使得点A落在CD边上的点E处,折痕为MN.若CE的长为7cm,则MN的长为( )| A. | 10 | B. | 13 | C. | 15 | D. | 无法求出 |
15.a2•a2÷a-2的结果是( )
| A. | a2 | B. | a5 | C. | a6 | D. | a7 |




 已知在△ABC中,AB=AC,AD⊥BC,AD与中线BE相交于点G,AD=18,GE=5,求BC的长.
已知在△ABC中,AB=AC,AD⊥BC,AD与中线BE相交于点G,AD=18,GE=5,求BC的长.