题目内容
1.问题背景如图1,在正方形ABCD的内部,作∠DAE=∠ABF=∠BCG=∠CDH,根据三角形全等的条件,易得△DAE≌△ABF≌△BCG≌△CDH,从而得到四边形EFGH是正方形.
类比探究
如图2,在正△ABC的内部,作∠BAD=∠CBE=∠ACF,AD,BE,CF两两相交于D,E,F三点(D,E,F三点不重合)

(1)△ABD,△BCE,△CAF是否全等?如果是,请选择其中一对进行证明.
(2)△DEF是否为正三角形?请说明理由.
(3)进一步探究发现,△ABD的三边存在一定的等量关系,设BD=a,AD=b,AB=c,请探索a,b,c满足的等量关系.
分析 (1)由正三角形的性质得出∠CAB=∠ABC=∠BCA=60°,AB=BC,证出∠ABD=∠BCE,由ASA证明△ABD≌△BCE即可;
(2)由全等三角形的性质得出∠ADB=∠BEC=∠CFA,证出∠FDE=∠DEF=∠EFD,即可得出结论;
(3)作AG⊥BD于G,由正三角形的性质得出∠ADG=60°,在Rt△ADG中,DG=$\frac{1}{2}$b,AG=$\frac{\sqrt{3}}{2}$b,在Rt△ABG中,由勾股定理即可得出结论.
解答 解:(1)△ABD≌△BCE≌△CAF;理由如下:
∵△ABC是正三角形,
∴∠CAB=∠ABC=∠BCA=60°,AB=BC,
∵∠ABD=∠ABC-∠2,∠BCE=∠ACB-∠3,∠2=∠3,
∴∠ABD=∠BCE,
在△ABD和△BCE中,$\left\{\begin{array}{l}{∠1=∠2}&{\;}\\{AB=BC}&{\;}\\{∠ABD=∠BCE}&{\;}\end{array}\right.$,
∴△ABD≌△BCE(ASA);
(2)△DEF是正三角形;理由如下:
∵△ABD≌△BCE≌△CAF,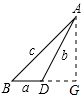
∴∠ADB=∠BEC=∠CFA,
∴∠FDE=∠DEF=∠EFD,
∴△DEF是正三角形;
(3)作AG⊥BD于G,如图所示:
∵△DEF是正三角形,
∴∠ADG=60°,
在Rt△ADG中,DG=$\frac{1}{2}$b,AG=$\frac{\sqrt{3}}{2}$b,
在Rt△ABG中,c2=(a+$\frac{1}{2}$b)2+($\frac{\sqrt{3}}{2}$b)2,
∴c2=a2+ab+b2.
点评 本题是综合题目,考查了正三角形的判定与性质、全等三角形的判定与性质、勾股定理等知识;本题综合性强,熟练掌握正三角形的判定与性质,证明三角形全等是解决问题的关键.

 金牌教辅培优优选卷期末冲刺100分系列答案
金牌教辅培优优选卷期末冲刺100分系列答案| A. | y=-3x+2 | B. | y=2x+1 | C. | y=2x2+1 | D. | y=-$\frac{1}{x}$ |
| A. | a8÷a4=a2 | B. | (2a2)3=6a6 | C. | 3a3-2a2=a | D. | 3a(1-a)=3a-3a2 |
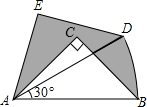 如图,在Rt△ABC中,∠ACB=90°,AC=BC=1,将Rt△ABC绕点A逆时针旋转30°后得到Rt△ADE,点B经过的路径为$\widehat{BD}$,则图中阴影部分的面积是( )
如图,在Rt△ABC中,∠ACB=90°,AC=BC=1,将Rt△ABC绕点A逆时针旋转30°后得到Rt△ADE,点B经过的路径为$\widehat{BD}$,则图中阴影部分的面积是( )| A. | $\frac{π}{6}$ | B. | $\frac{π}{3}$ | C. | $\frac{π}{2}$-$\frac{1}{2}$ | D. | $\frac{1}{2}$ |
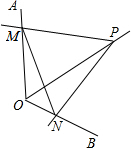 如图,点P为定角∠AOB的平分线上的一个定点,且∠MPN与∠AOB互补,若∠MPN在绕点P旋转的过程中,其两边分别与OA、OB相交于M、N两点,则以下结论:(1)PM=PN恒成立;(2)OM+ON的值不变;(3)四边形PMON的面积不变;(4)MN的长不变,其中正确的个数为( )
如图,点P为定角∠AOB的平分线上的一个定点,且∠MPN与∠AOB互补,若∠MPN在绕点P旋转的过程中,其两边分别与OA、OB相交于M、N两点,则以下结论:(1)PM=PN恒成立;(2)OM+ON的值不变;(3)四边形PMON的面积不变;(4)MN的长不变,其中正确的个数为( )