题目内容
正多边形的一个内角等于144°，则该多边形是正（ ）边形．
| A、8 | B、9 | C、10 | D、11 |
考点：多边形内角与外角
专题：
分析：根据正多边形的每个内角相等，可得正多边形的内角和，再根据多边形的内角和公式，可得答案．
解答：解：设正多边形是n边形，由题意得
（n-2）×180°=144°n．
解得n=10，
故选；C．
（n-2）×180°=144°n．
解得n=10，
故选；C．
点评：本题考查了多边形的内角与外角，利用了正多边形的内角相等，多边形的内角和公式．
练习册系列答案
相关题目
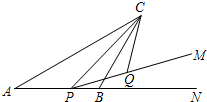如图，△ABC中，AC=10，∠BAC=30°，点P是射线AB上的一个动点，cos∠CPM=
已知点P为⊙O所在平面上一点，过点P的两条直线PA，PC分别交⊙O于A，B和C，D两点，且PO平分∠APC．求证：PA=PC．
下列各数中：+5、-2.5、-
、2、
、-（-7）、0、-|+3|，负有理数有（ ）
| 4 |
| 3 |
| 7 |
| 5 |
| A、2个 | B、3个 | C、4个 | D、5个 |