题目内容
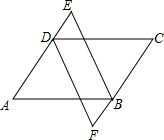如图所示，在四边形ABCD中，已知AB=CD，AD=BC，DE=BF，且点E、F分别在AD、CB的延长线上．求证：BE=DF．考点：全等三角形的判定与性质
专题：证明题
分析：由AB=CD，AD=BC，得出四边形ABCD是平行四边形，得出AD∥BC，即得出DE∥BF，再由DE=BF，得出四边形DEBF是平行四边形，进一步得出结论即可．
解答：解：∵AB=CD，AD=BC，
∴四边形ABCD是平行四边形，
∴AD∥BC，
∴DE∥BF，
又∵DE=BF，
∴四边形DEBF是平行四边形，
∴BE=DF．
∴四边形ABCD是平行四边形，
∴AD∥BC，
∴DE∥BF，
又∵DE=BF，
∴四边形DEBF是平行四边形，
∴BE=DF．
点评：此题考查平行四边形的判定与性质，掌握平行四边形的基本判定方法是解决问题的关键．
练习册系列答案
阅读快车系列答案
相关题目
下列不是同类项的是（ ）
| A、-a2b2与4a2b2 | ||
B、xy与
| ||
| C、4与-5 | ||
| D、3a2b与3ab2 |
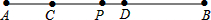如图所示，C，D是线段AB上的两点，AC：CD：DB=2：3：4，P是线段AB的中点，若PD=2厘米，求：
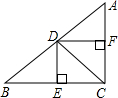如图，在Rt△ABC中，∠ACB=90°，CD平分∠ACB，过点D分别作DE⊥BC，DF⊥AC，垂足分别为E，F．
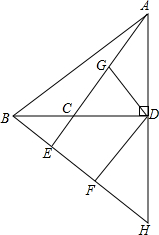已知，如图，在钝角△ABC中，BE和AD分别是AC和BC边上的高，BE和AD的延长线交于点H，点F、G分别是BH、AC的中点．
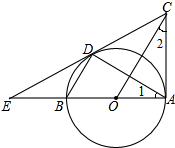已知A、D为⊙O的切点，AB为直径，延长AB交D所在的切线于点E，A所在的切线交于点C．求证：