题目内容
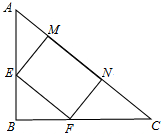 如图,在Rt△ABC中,AC=40,BC=30,在其内部挖出一个矩形,问挖出的矩形的最大面积是多少?
如图,在Rt△ABC中,AC=40,BC=30,在其内部挖出一个矩形,问挖出的矩形的最大面积是多少?考点:相似三角形的判定与性质,二次函数的最值
专题:
分析:设EM=x,利用平行线分线段成比例表示出EF,可得到矩形的面积关于x的二次函数,用二次函数的性质求出其最大值即可.
解答:解:在Rt△ABC中可求得AB=10
,过B作BD⊥AC于点D,交EF于点G,
利用面积相等可得AC•BD=AB•BC,解得BD=
设EM=x,则BG=BD-DG=BD-EM=
-x,且AC=40,
∵EF∥AC,
∴
=
,即
=
,解得EF=40-
x,
∴S矩形EFNM=EF•EM=x(40-
x)=-
x2+40x,
该二次函数开口向下,
∴当x=
时,有最大值75
.
即挖出的矩形的最大面积为75
.
| 7 |
利用面积相等可得AC•BD=AB•BC,解得BD=
30
| ||
| 4 |
设EM=x,则BG=BD-DG=BD-EM=
30
| ||
| 4 |
∵EF∥AC,
∴
| EF |
| AC |
| BG |
| BD |
| EF |
| 40 |
| ||||
|
16
| ||
| 21 |
∴S矩形EFNM=EF•EM=x(40-
16
| ||
| 21 |
16
| ||
| 21 |
该二次函数开口向下,
∴当x=
15
| ||
| 4 |
| 7 |
即挖出的矩形的最大面积为75
| 7 |
点评:本题主要考查平行线分线段成比例及函数的最值,利用x分别表示出EF、EM得到关于x的二次函数是解题的关键.注意方程思想的应用.

练习册系列答案
相关题目
 如图所示,在△ABC中,D是BC延长线上一点,∠B=38°,∠A=62°,则∠ACD等于( )
如图所示,在△ABC中,D是BC延长线上一点,∠B=38°,∠A=62°,则∠ACD等于( )| A、24° | B、38° |
| C、62° | D、100° |
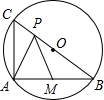 如图,BC为⊙O的直径,BC=2
如图,BC为⊙O的直径,BC=2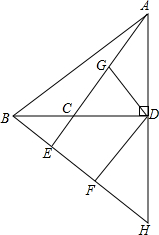 已知,如图,在钝角△ABC中,BE和AD分别是AC和BC边上的高,BE和AD的延长线交于点H,点F、G分别是BH、AC的中点.
已知,如图,在钝角△ABC中,BE和AD分别是AC和BC边上的高,BE和AD的延长线交于点H,点F、G分别是BH、AC的中点. 如图,AB是⊙O的切线,切点为C,则图中成立的结论有
如图,AB是⊙O的切线,切点为C,则图中成立的结论有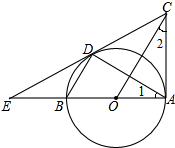 已知A、D为⊙O的切点,AB为直径,延长AB交D所在的切线于点E,A所在的切线交于点C.求证:
已知A、D为⊙O的切点,AB为直径,延长AB交D所在的切线于点E,A所在的切线交于点C.求证: