题目内容
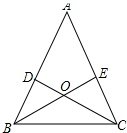 如图,在等腰三角形ABC中,两底角的平分线BE、CD相交于点O,求证:OB=0C,OD=OE.
如图,在等腰三角形ABC中,两底角的平分线BE、CD相交于点O,求证:OB=0C,OD=OE.考点:等腰三角形的性质,全等三角形的判定与性质
专题:证明题
分析:首先根据等边对等角可得∠ABC=∠ACB,然后根据角平分线的性质可得∠OBC=
∠ABC,∠OCB=
∠ACB,进而得到∠OBC=∠OCB,再根据等角对等边可得OB=0C;再根据ASA证明△OBD≌△OCE,由全等三角形的对应边相等即可得到OD=OE.
| 1 |
| 2 |
| 1 |
| 2 |
解答:证明:∵AB=AC,
∴∠ABC=∠ACB,
∵BD、CE是角平分线,它们相交于点O,
∴∠OBC=∠OBD=
∠ABC,∠OCB=∠OCE=
∠ACB,
∴∠OBC=∠OCB,
∴OB=0C;
在△OBD与△OCE中,
,
∴△OBD≌△OCE(ASA),
∴OD=OE.
∴∠ABC=∠ACB,
∵BD、CE是角平分线,它们相交于点O,
∴∠OBC=∠OBD=
| 1 |
| 2 |
| 1 |
| 2 |
∴∠OBC=∠OCB,
∴OB=0C;
在△OBD与△OCE中,
|
∴△OBD≌△OCE(ASA),
∴OD=OE.
点评:此题主要考查了等腰三角形的判定与性质,角平分线定义,全等三角形的判定与性质,难度适中.得出∠OBC=∠OCB是解题的关键.

练习册系列答案
相关题目
 如图,在△ABC中,AB∥y轴,AB=2,点B(-3,1),BC=1且BC∥x轴.
如图,在△ABC中,AB∥y轴,AB=2,点B(-3,1),BC=1且BC∥x轴. 如图,喷水池的喷水口位于水池中心,离水面高为0.5m,喷出水柱呈抛物线,最高点离水面
如图,喷水池的喷水口位于水池中心,离水面高为0.5m,喷出水柱呈抛物线,最高点离水面