题目内容
 如图,在△ABC中,AB∥y轴,AB=2,点B(-3,1),BC=1且BC∥x轴.
如图,在△ABC中,AB∥y轴,AB=2,点B(-3,1),BC=1且BC∥x轴.(1)试写出A、C两点的坐标;
(2)作出△A1B1C1,使△A1B1C1和△ABC关于y轴对称;
(3)求以点A、C、C1、A1为顶点的四边形的面积.
考点:作图-轴对称变换
专题:
分析:(1)利用AB=2,以及B点坐标,即可得出A,C点坐标;
(2)利用关于y轴对称点的性质得出答案;
(3)利用对称点性质以及梯形面积公式求出即可.
(2)利用关于y轴对称点的性质得出答案;
(3)利用对称点性质以及梯形面积公式求出即可.
解答: 解:(1)∵AB∥y轴,AB=2,点B(-3,1),BC=1且BC∥x轴,
解:(1)∵AB∥y轴,AB=2,点B(-3,1),BC=1且BC∥x轴,
∴A(-3,3),C(-2,1);
(2)如图所示:△A1B1C1即为所求;
(3)以点A、C、C1、A1为顶点的四边形的面积为:
(AA1+CC1)×AB=
×(3+3)×2=6.
 解:(1)∵AB∥y轴,AB=2,点B(-3,1),BC=1且BC∥x轴,
解:(1)∵AB∥y轴,AB=2,点B(-3,1),BC=1且BC∥x轴,∴A(-3,3),C(-2,1);
(2)如图所示:△A1B1C1即为所求;
(3)以点A、C、C1、A1为顶点的四边形的面积为:
| 1 |
| 2 |
| 1 |
| 2 |
点评:此题主要考查了轴对称变换以及梯形面积公式应用,得出对应点坐标是解题关键.

练习册系列答案
相关题目
 如图所示,已知五边形ABCDE,O点是五边形ABCDE内一点,A1,B1,C1,D1,E1分别是OA,OB,OC,OD,OE上的点,且A1B1∥AB,B1C1∥BC,C1D1∥CD,D1E1∥DE,A1E1∥AE.若OD=2OD1,S五边形ABCDE=100cm2,求五边形A1B1C1D1E1的面积.
如图所示,已知五边形ABCDE,O点是五边形ABCDE内一点,A1,B1,C1,D1,E1分别是OA,OB,OC,OD,OE上的点,且A1B1∥AB,B1C1∥BC,C1D1∥CD,D1E1∥DE,A1E1∥AE.若OD=2OD1,S五边形ABCDE=100cm2,求五边形A1B1C1D1E1的面积.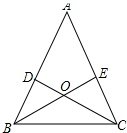 如图,在等腰三角形ABC中,两底角的平分线BE、CD相交于点O,求证:OB=0C,OD=OE.
如图,在等腰三角形ABC中,两底角的平分线BE、CD相交于点O,求证:OB=0C,OD=OE.