题目内容
“无论x取何实数，代数式x2+y2-12x+8y+53的值总为正数”，这种说法对吗？请说说你的理由．
考点：配方法的应用,非负数的性质：偶次方
专题：
分析：先把原代数式利用配方法转化为x2+y2-12x+8y+53=（x-6）2+（y+4）2+1的形式，然后根据非负数的性质来讨论代数式x2+y2-12x+8y+53的值的正负．
解答：解：∵x2+y2-12x+8y+53，
=x2-12x+36+y2+8y+16+1，
=（x-6）2+（y+4）2+1；
无论x，y取何值，（x-6）2≥0，（y+4）2≥0，
故（x-6）2+（y+4）2+1≥1＞0．
因此代数式的值总是正数．
=x2-12x+36+y2+8y+16+1，
=（x-6）2+（y+4）2+1；
无论x，y取何值，（x-6）2≥0，（y+4）2≥0，
故（x-6）2+（y+4）2+1≥1＞0．
因此代数式的值总是正数．
点评：本题考查了配方法的应用、非负数的性质--偶次方．解题时要注意配方法的步骤．注意在变形的过程中不要改变式子的值．
练习册系列答案
相关题目
如图所示，已知五边形ABCDE，O点是五边形ABCDE内一点，A1，B1，C1，D1，E1分别是OA，OB，OC，OD，OE上的点，且A1B1∥AB，B1C1∥BC，C1D1∥CD，D1E1∥DE，A1E1∥AE．若OD=2OD1，S五边形ABCDE=100cm2，求五边形A1B1C1D1E1的面积．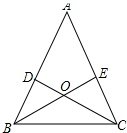
如图，在等腰三角形ABC中，两底角的平分线BE、CD相交于点O，求证：OB=0C，OD=OE．