题目内容
9.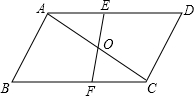 如图所示,已知△ABC与△CDA关于点O对称,过O任作直线EF分别交AD、BC于点E、F,下面的结论:
如图所示,已知△ABC与△CDA关于点O对称,过O任作直线EF分别交AD、BC于点E、F,下面的结论:①点E和点F,点B和点D是关于中心O对称点;
②直线BD必经过点O;
③四边形DEOC与四边形BFOA的面积必相等;
④△AOE与△COF成中心对称.
其中正确的个数为( )
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
分析 由于△ABC与△CDA关于点O对称,那么可得到AB=CD、AD=BC,即四边形ABCD是平行四边形,由于平行四边形是中心对称图形,且对称中心是对角线交点,据此对各结论进行判断.
解答 解:△ABC与△CDA关于点O对称,则AB=CD、AD=BC,
所以四边形ABCD是平行四边形,即点O就是?ABCD的对称中心,则有:
(1)点E和点F,B和D是关于中心O的对称点,正确;
(2)直线BD必经过点O,正确;
(3)四边形DEOC与四边形BFOA的面积必相等,正确;
(5)△AOE与△COF成中心对称,正确;
其中正确的个数为4个,
故选D.
点评 本题主要考查了中心对称的性质以及平行四边形的性质的运用,熟练掌握平行四边形的性质及中心对称图形的性质是解决此题的关键.解题时注意:关于中心对称的两个图形,对应点的连线都经过对称中心,并且被对称中心平分.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
17.方程$\frac{x+2}{4}$+1=$\frac{x}{3}$,去分母后正确的是( )
| A. | 3(x+2)+12=4x | B. | 12(x+2)+12=12x | C. | 4(x+2)+12=3x | D. | 3(x+2)+1=4x |
14.在平面直角坐标系中,⊙O的半径为5,圆心O为坐标原点,则点P(3,-4)与⊙O的位置关系是( )
| A. | 点P在⊙O上 | B. | 点P在⊙O外部 | C. | 点P在⊙O内部 | D. | 不能确定 |
18.在△ABC中,∠C=90°,AC=3,CB=4,则cotA的值为( )
| A. | $\frac{4}{5}$ | B. | $\frac{3}{5}$ | C. | $\frac{4}{3}$ | D. | $\frac{3}{4}$ |
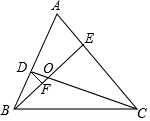 已知:如图,在等边△ABC中,点D、E分别在AB、AC上,且BD=AE,CD交BE于点O,DF⊥BE,点F为垂足.
已知:如图,在等边△ABC中,点D、E分别在AB、AC上,且BD=AE,CD交BE于点O,DF⊥BE,点F为垂足.