题目内容
20.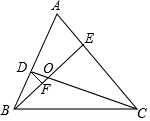 已知:如图,在等边△ABC中,点D、E分别在AB、AC上,且BD=AE,CD交BE于点O,DF⊥BE,点F为垂足.
已知:如图,在等边△ABC中,点D、E分别在AB、AC上,且BD=AE,CD交BE于点O,DF⊥BE,点F为垂足.(1)求证:∠ABE=∠BCD;
(2)求证:OD=2OF.
分析 (1)根据等边三角形的性质可得出AB=BC、∠A=∠CBD=60°,结合AE=BD即可证出△ABE≌△BCD(SAS),进而即可得出∠ABE=∠BCD;
(2)由(1)可知∠AEB=∠BDC,结合∠ABE=∠OBD即可得出△ABE∽△ODE,进而得出∠BOD=∠A=60°,在Rt△ODF中,通过特殊角的余弦值即可证出OD=2OF.
解答 证明:(1)∵△ABC为等边三角形,
∴AB=BC,∠A=∠CBD=60°.
在△ABE和△BCD中,$\left\{\begin{array}{l}{AB=BC}\\{∠A=∠CBD}\\{AE=BD}\end{array}\right.$,
∴△ABE≌△BCD(SAS),
∴∠ABE=∠BCD.
(2)∵△ABE≌△BCD,
∴∠AEB=∠BDC.
∵∠ABE=∠OBD,
∴△ABE∽△ODE,
∴∠BOD=∠A=60°.
在Rt△ODF中,DF⊥BE,∠DOF=60°,
∴$\frac{OF}{OD}=cos∠DOF$=$\frac{1}{2}$,
∴OD=2OF.
点评 本题考查了全等三角形的判定与性质、等边三角形的性质以及相似三角形的判定与性质,熟练掌握全等(相似)三角形的判定与性质是解题的关键.

练习册系列答案
 黄冈创优卷系列答案
黄冈创优卷系列答案
相关题目
10.把下列各式约分:
| (1)$\frac{{a}^{2}-ab}{a-b}$ | (2)$\frac{2{x}^{4}-4{x}^{3}}{x-2}$ | (3)$\frac{{x}^{2}-25}{{x}^{2}-5x}$ |
| (4)$\frac{-(2-x)}{-(y-2)(x-2)}$ | (5)$\frac{{x}^{2}+6x+9}{{x}^{2}-9}$ | (6)$\frac{{m}^{2}-8m+16}{{m}^{2}-4m}$ |
11.比较-$\frac{1}{3}$,-$\frac{1}{4}$,$\frac{1}{6}$的大小,结果正确的是( )
| A. | $\frac{1}{6}<-\frac{1}{4}<-\frac{1}{3}$ | B. | $\frac{1}{6}<-\frac{1}{3}<-\frac{1}{4}$ | C. | $-\frac{1}{4}<-\frac{1}{3}<\frac{1}{6}$ | D. | $-\frac{1}{3}<-\frac{1}{4}<\frac{1}{6}$ |
15.下列说法中正确的个数是( )
①1是单项式;
②单项式-$\frac{ab}{2}$的系数是-1,次数是2;
③多项式x2+x-1的常数项是1;
④多项式x2+2xy+y2的次数是2.
①1是单项式;
②单项式-$\frac{ab}{2}$的系数是-1,次数是2;
③多项式x2+x-1的常数项是1;
④多项式x2+2xy+y2的次数是2.
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
5.某冰箱降价30%后,每台售价a元,则该冰箱每台原价应为( )
| A. | 0.3a元 | B. | 0.7a元 | C. | $\frac{10a}{3}$元 | D. | $\frac{10a}{7}$元 |
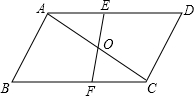 如图所示,已知△ABC与△CDA关于点O对称,过O任作直线EF分别交AD、BC于点E、F,下面的结论:
如图所示,已知△ABC与△CDA关于点O对称,过O任作直线EF分别交AD、BC于点E、F,下面的结论: 已知△ABC,∠A=60°,BC=6.
已知△ABC,∠A=60°,BC=6.