��Ŀ����
18�� ��ͼ����֪�����ϵ�A��ʾ����Ϊ6��B��������һ�㣬��AB�ij���Ϊ10������P�ӵ�A��������ÿ��6����λ���ȵ��ٶ����������������˶������˶�ʱ��Ϊt��t��0���룬
��ͼ����֪�����ϵ�A��ʾ����Ϊ6��B��������һ�㣬��AB�ij���Ϊ10������P�ӵ�A��������ÿ��6����λ���ȵ��ٶ����������������˶������˶�ʱ��Ϊt��t��0���룬��1��д�������ϵ�B����ʾ������-4��
��2����t=$\frac{1}{2}$ʱ��P������ʾ������3����t=2ʱ��P������ʾ������-6��t��ʱ����P����ʾ����6-6t�����ú�t�Ĵ���ʽ��ʾ����
��3��M��AP���е㣬NΪPB���е㣬��P���˶��Ĺ����У��߶�MN�ij����Ƿ����仯�����仯��˵�����ɣ������䣬���㻭��ͼ�Σ�������߶�MN�ij���
���� ��1��B���ʾ����Ϊ6-10=-4��
��2�����������������ľ��빫ʽ�������������⣬�ٸ��������ϵ���˶��Ϳ������P������ꣻ
��3���������ۣ��ٵ���P�ڵ�A��B����֮���˶�ʱ���ڵ���P�˶�����B�����ʱ�������е�Ķ�����߶εĺͲ������MN��
��� �⣺��1��B���ʾ����Ϊ6-10=-4��
�ʴ�Ϊ+-4��
��2���ߵ�t=$\frac{1}{2}$ʱ��P������ʾ������3����t=2ʱ��P������ʾ������-6��t��ʱ����P��ʾ����Ϊ��6-6t��
�ʴ�Ϊ��3��-6��6-6t��
��3���߶�MN�ij��Ȳ������仯��
���ɣ������������
�ٵ���P��A��B����֮���˶�ʱ����ͼ��
MN=MP+NP=$\frac{1}{2}$BP+$\frac{1}{2}$PA=$\frac{1}{2}$AB=5��
�ڵ���P�˶�����B�����ʱ����ͼ��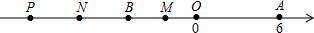
MN=MP-NP=$\frac{1}{2}$AP-$\frac{1}{2}$PB=$\frac{1}{2}$AB=5��
�����������߶�MN�ij��Ȳ������仯����ֵΪ5��
���� ���⿼���������ľ��룬������֪�ó����߶�֮��ĵ�����ϵ�ǽ���ؼ���ע��ڶ�����Ҫ�������ۣ�

��ϰ��ϵ�д�
 �Ķ��쳵ϵ�д�
�Ķ��쳵ϵ�д�
�����Ŀ
6�����ڶ��κ��� y=��x-1��2+2 ��ͼ������˵����ȷ���ǣ�������
| A�� | �������� | B�� | ���������ǣ�-1��2�� | ||
| C�� | �Գ����� x=1 | D�� | �� x ������������ |
10��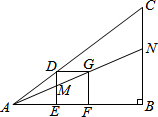 ��ͼ��ABC����һ������DEFG������D��AC�ϣ�E��F��AB�ϣ�ֱ��AG�ֱ�DE��BC��M��N���㣮����B=90�㣬AC=5��BC=3��DG=1����BN�ij���Ϊ��������
��ͼ��ABC����һ������DEFG������D��AC�ϣ�E��F��AB�ϣ�ֱ��AG�ֱ�DE��BC��M��N���㣮����B=90�㣬AC=5��BC=3��DG=1����BN�ij���Ϊ��������
 ��ͼ��ABC����һ������DEFG������D��AC�ϣ�E��F��AB�ϣ�ֱ��AG�ֱ�DE��BC��M��N���㣮����B=90�㣬AC=5��BC=3��DG=1����BN�ij���Ϊ��������
��ͼ��ABC����һ������DEFG������D��AC�ϣ�E��F��AB�ϣ�ֱ��AG�ֱ�DE��BC��M��N���㣮����B=90�㣬AC=5��BC=3��DG=1����BN�ij���Ϊ��������| A�� | $\frac{4}{3}$ | B�� | $\frac{3}{2}$ | C�� | $\frac{8}{5}$ | D�� | $\frac{12}{7}$ |
7����֪m�Ƿ���x2-x-2=0��һ�����������ʽm2-m+3=��������
| A�� | -2 | B�� | 1 | C�� | 0 | D�� | 5 |
8�����з����У���һԪһ�η��̵��ǣ�������
| A�� | x2-4x=3 | B�� | 3��x+2��=6 | C�� | x+2y=1 | D�� | x-1=$\frac{1}{x}$ |
 ��ֱ�ǡ�ABC�У���C=90�㣬AC=30cm��BC=40cm������M�ӵ�C��������2cm/s���ٶȴ�C��B�˶������M���˶�ʱ��Ϊt����λ���룩��
��ֱ�ǡ�ABC�У���C=90�㣬AC=30cm��BC=40cm������M�ӵ�C��������2cm/s���ٶȴ�C��B�˶������M���˶�ʱ��Ϊt����λ���룩��