题目内容
 如图,点A、B、C在⊙O上,∠ACB=60°,则∠OAB的度数是
如图,点A、B、C在⊙O上,∠ACB=60°,则∠OAB的度数是考点:圆周角定理
专题:
分析:延长AO交⊙O于D,连接BD,根据圆周角定理可得∠ADB=60°,∠ABD=90°,再利用三角形内角和定理可得答案.
解答: 解:延长AO交⊙O于D,连接BD,
解:延长AO交⊙O于D,连接BD,
∵∠ACB=60°,
∴∠ADB=60°,
∵AD为直径,
∴∠ABD=90°,
∴∠OAB=180°-90°-60°=30°,
故答案为:30°.
 解:延长AO交⊙O于D,连接BD,
解:延长AO交⊙O于D,连接BD,∵∠ACB=60°,
∴∠ADB=60°,
∵AD为直径,
∴∠ABD=90°,
∴∠OAB=180°-90°-60°=30°,
故答案为:30°.
点评:此题主要考查了圆周角定理,关键是掌握圆周角定理:在同圆或等圆中,同弧或等弧所对的圆周角相等,都等于这条弧所对的圆心角的一半.
推论:半圆(或直径)所对的圆周角是直角,90°的圆周角所对的弦是直径.
推论:半圆(或直径)所对的圆周角是直角,90°的圆周角所对的弦是直径.

练习册系列答案
相关题目
 已知:如图,E是AC上一点,AB=CE,AB∥CD,∠ACB=∠D.求证:BC=ED.
已知:如图,E是AC上一点,AB=CE,AB∥CD,∠ACB=∠D.求证:BC=ED.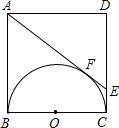 在边长为a的正方形内ABCD中,AE与以BC为直径的半圆相切于点F,交CD于E,求CF、FD的长.
在边长为a的正方形内ABCD中,AE与以BC为直径的半圆相切于点F,交CD于E,求CF、FD的长. 如图,以等腰直角△ABC两锐角顶点A、B为圆心作等圆,⊙A与⊙B恰好外切,若AC=2,那么图中两个扇形(即阴影部分)的面积之和为
如图,以等腰直角△ABC两锐角顶点A、B为圆心作等圆,⊙A与⊙B恰好外切,若AC=2,那么图中两个扇形(即阴影部分)的面积之和为 如图,在Rt△ABC中,BC=8,AC=6,∠ACB=90°,分别以A、B为圆心作两个外切的等圆,则图中阴影部分的面积是
如图,在Rt△ABC中,BC=8,AC=6,∠ACB=90°,分别以A、B为圆心作两个外切的等圆,则图中阴影部分的面积是 如图,在四边形ABCD中,AD∥BC,∠BCD=90°,∠ABC=45°,AD=CD,CE平分∠ACB交AB于点E,在BC上截取BF=AE,连接AF交CE于点G,连接DG交AC于点H,过点A作AN⊥BC,垂足为N,AN交CE于点M.则下列结论:
如图,在四边形ABCD中,AD∥BC,∠BCD=90°,∠ABC=45°,AD=CD,CE平分∠ACB交AB于点E,在BC上截取BF=AE,连接AF交CE于点G,连接DG交AC于点H,过点A作AN⊥BC,垂足为N,AN交CE于点M.则下列结论: 如图,将△OAB绕点O沿顺时针方向旋转90°后得到△OA1B1,若OA=3,则AA1=
如图,将△OAB绕点O沿顺时针方向旋转90°后得到△OA1B1,若OA=3,则AA1=