题目内容
18.下面一列数是按照某种规律排列的:$\frac{1}{2},-\frac{2}{10},\frac{3}{26},-\frac{4}{50},…$,则第7个数是$\frac{7}{170}$.分析 根据所给出的数据可得,分子是从1开始的连续自然数,分母是依次是12+1,22+1,32+1,42+1,并且第奇数个数是正数,第偶数个数是负数,然后写出第7个数即可.
解答 解:∵$\frac{1}{2},-\frac{2}{10},\frac{3}{26},-\frac{4}{50},…$,
观察分子、分母可以看出规律,$\frac{1}{{1}^{2}+1}$,-$\frac{2}{{3}^{2}+1}$,$\frac{3}{{5}^{2}+1}$,-$\frac{4}{{7}^{2}+1}$,奇数个数是正数,偶数个数是负数,
∴第7个数是$\frac{7}{1{3}^{2}+1}$=$\frac{7}{170}$.
故答案为:$\frac{7}{170}$.
点评 本题是对数字变化规律的考查,难点在于观察出分子、分母的变化规律.

练习册系列答案
 互动课堂系列答案
互动课堂系列答案 激活思维智能训练课时导学练系列答案
激活思维智能训练课时导学练系列答案
相关题目
8.已知2011x2014+2012x2013+2013x2012+2014=1021x2014+1022x2013+1023x2012-956,那么x2014+x2013+x2012-1的值为( )
| A. | -44 | B. | -34 | C. | -24 | D. | -14 |
6.下列各式中,一定成立的是( )
| A. | -22=|-22| | B. | 23=(-2)3 | C. | 22=(-2)2 | D. | (-2)3=|(-2)3| |
 将连续正整数1,2,3,4…按如图的规律排列,则数字2014在第12行,第45列.
将连续正整数1,2,3,4…按如图的规律排列,则数字2014在第12行,第45列.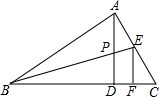 如图,在△ABC中,∠BAC=90°,AD⊥BC于点D,P是AD的中点,BP交AC于点E,EF⊥BC于点F,若AE=3,EC=4,求EF的值.
如图,在△ABC中,∠BAC=90°,AD⊥BC于点D,P是AD的中点,BP交AC于点E,EF⊥BC于点F,若AE=3,EC=4,求EF的值.