题目内容
如图，把一张长方形纸片ABCD沿EF折叠后，ED交BC于点G，点D、C分别落在D′、C′位置上，若∠EFC′=130°，那么∠AEG=考点：平行线的性质,翻折变换（折叠问题）
专题：
分析：根据DE'∥C'F可以得到∠FEG=180°-∠EFC'=50°，然后根据折叠的性质可得∠DEF=∠FEG=50°，则∠AEG即可求得．
解答：解：∵DE'∥C'F，
∴∠FEG=180°-∠EFC'=50°，
又∵∠DEF=∠FEG=50°，
∴∠AEG=180°-∠DEF-∠FEG=80°．
故答案是：80．
∴∠FEG=180°-∠EFC'=50°，
又∵∠DEF=∠FEG=50°，
∴∠AEG=180°-∠DEF-∠FEG=80°．
故答案是：80．
点评：本题考查图形的翻折变换，解题过程中应注意折叠是一种对称变换，它属于轴对称，根据轴对称的性质，折叠前后图形的形状和大小不变，如本题中折叠前后对应角相等．
练习册系列答案
相关题目
已知在正方形网格中，每个小方格都是边长为1的正方形，A、B两点在小方格的顶点上，位置如图，点C也在小方格的顶点上，且以A、B、C为顶点的三角形的面积为1个平方单位，则点C的个数为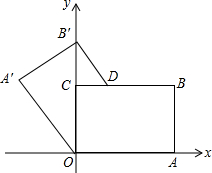
如图，矩形OABC的顶点O是坐标原点，顶点A、C分别在x轴、y轴的正半轴上，顶点B在第一象限，OA=8，OC=6，点D在边BC上，将四边形OABD沿直线OD翻折，使点A和点B分别落在这个坐标平面的点A′和点B′处，且点B′刚好落在y轴上．若某反比例函数的图象经过点A′，则这个反比例函数的解析式为sin47°、tan47°、cos47°的大小关系是（ ）
| A、cos47°＞sin47°＞tan47° |
| B、tan47°＞sin47°＞cos47° |
| C、sin47°＞tan47°＞cos47° |
| D、tan47°＞cos47°＞sin47° |
用两个完全相同的长方体搭成如图的几何体，这个几何体的主视图是（ ）A、 |
B、 |
C、 |
D、 |
下列语句中，不是命题的是（ ）
| A、两点确定一条直线 |
| B、垂线段最短 |
| C、同位角相等 |
| D、做角A的平分线 |