题目内容
12.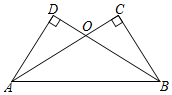 已知:AC⊥BC,BD⊥AD,AC 与BD 交于O,AC=BD,∠CAB=32°.求∠DAB的度数.
已知:AC⊥BC,BD⊥AD,AC 与BD 交于O,AC=BD,∠CAB=32°.求∠DAB的度数.
分析 根据全等三角形的判定可得Rt△ABC≌Rt△BAD(HL),即可求得∠DAB的度数.
解答 证明:∵AC⊥BC,BD⊥AD,
∴∠C=∠D=90°,
∴在Rt△ABC和Rt△BAD中,$\left\{\begin{array}{l}AB=BA(公共边)\\ AC=BD\end{array}\right.$,
∴Rt△ABC≌Rt△BAD(HL),
∴∠CAB=∠DBA,
∵∠CAB=32°,
∴∠DBA=32°.
在Rt△BAD中,∠DAB=90°-∠DBA,
∴∠DAB=90°-32°=58°.
点评 此题考查三角形全等的判定与性质,利用全等三角形的性质证明∠CAB=∠DBA是解决问题的关键.

练习册系列答案
相关题目
4. 点A、B、C、D都在如图所示的由正方形组成的网格图中,且线段CD与线段AB成位似图形,则位似中心为( )
点A、B、C、D都在如图所示的由正方形组成的网格图中,且线段CD与线段AB成位似图形,则位似中心为( )
 点A、B、C、D都在如图所示的由正方形组成的网格图中,且线段CD与线段AB成位似图形,则位似中心为( )
点A、B、C、D都在如图所示的由正方形组成的网格图中,且线段CD与线段AB成位似图形,则位似中心为( )| A. | 点E | B. | 点F | C. | 点H | D. | 点G |
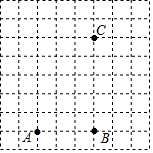 如图所示,已知点A、B、C是网格纸上的三个格点,根据要求画图或作答.
如图所示,已知点A、B、C是网格纸上的三个格点,根据要求画图或作答.