题目内容
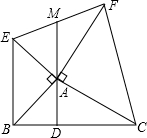 如图,在△ABC中,以AB、AC为直角边,分别向外作等腰Rt△ABE和等腰Rt△ACF,连接EF,过点A作AD⊥BC,垂足为D,反向延长DA交EF于点M.
如图,在△ABC中,以AB、AC为直角边,分别向外作等腰Rt△ABE和等腰Rt△ACF,连接EF,过点A作AD⊥BC,垂足为D,反向延长DA交EF于点M.(1)用圆规比较EM与FM的大小.
(2)证明(1)中的结论.
考点:全等三角形的判定与性质,等腰直角三角形
专题:计算题
分析:(1)利用圆规验证即可;
(2)作EH⊥AM,交AM于点H,FK⊥AM,交AM延长线于点K,利用同角的余角相等得到一对角相等,再由一对直角相等,且AE=AB,利用AAS得到三角形AEH与三角形ABD全等,利用全等三角形对应边相等得到EH=AD,同理得到三角形AFK与三角形ACD全等,得到AD=FK,等量代换得到FK=EH,再由一对直角相等且对顶角相等,利用AAS得到三角形FKM与三角形EHM全等,利用全等三角形对应边相等即可得证.
(2)作EH⊥AM,交AM于点H,FK⊥AM,交AM延长线于点K,利用同角的余角相等得到一对角相等,再由一对直角相等,且AE=AB,利用AAS得到三角形AEH与三角形ABD全等,利用全等三角形对应边相等得到EH=AD,同理得到三角形AFK与三角形ACD全等,得到AD=FK,等量代换得到FK=EH,再由一对直角相等且对顶角相等,利用AAS得到三角形FKM与三角形EHM全等,利用全等三角形对应边相等即可得证.
解答: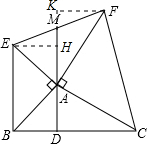 解:(1)利用圆规验证即可;
解:(1)利用圆规验证即可;
(2)证明:作EH⊥AM,交AM于点H,FK⊥AM,交AM延长线于点K,
∴∠AEH+∠EAH=90°,
∵∠EAB=90°,
∴∠EAH+∠BAD=90°,
∴∠AEH=∠BAD,
在△AEH和△BAD中,
,
∴△AEH≌△BAD(AAS),
∴EH=AD,
同理得到△AFK≌△ACD,
∴FK=AD,
∴FK=EH,
在△FKM和△EHM中,
,
∴△FKM≌△EHM(AAS),
∴FM=EM.
 解:(1)利用圆规验证即可;
解:(1)利用圆规验证即可;(2)证明:作EH⊥AM,交AM于点H,FK⊥AM,交AM延长线于点K,
∴∠AEH+∠EAH=90°,
∵∠EAB=90°,
∴∠EAH+∠BAD=90°,
∴∠AEH=∠BAD,
在△AEH和△BAD中,
|
∴△AEH≌△BAD(AAS),
∴EH=AD,
同理得到△AFK≌△ACD,
∴FK=AD,
∴FK=EH,
在△FKM和△EHM中,
|
∴△FKM≌△EHM(AAS),
∴FM=EM.
点评:此题考查了全等三角形的判定与性质,熟练掌握全等三角形的判定与性质是解本题的关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
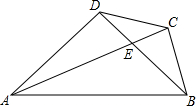 如图,在四边形ABCD中,AC与BD相交于点E,AD=BD,∠ADB=∠ACB=90°,AE=2BC.
如图,在四边形ABCD中,AC与BD相交于点E,AD=BD,∠ADB=∠ACB=90°,AE=2BC.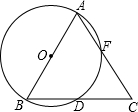 已知如图,以等腰△ABC的一腰AB为直径的⊙O交另一腰于F,交底边BC于D,探究BC与DF的关系,证明你的观点.
已知如图,以等腰△ABC的一腰AB为直径的⊙O交另一腰于F,交底边BC于D,探究BC与DF的关系,证明你的观点.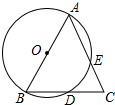 在△ABC中,AB=AC,以AB为直径的圆O分别交BC、AC于点D、E,
在△ABC中,AB=AC,以AB为直径的圆O分别交BC、AC于点D、E,