题目内容
利用配方法,把下列函数写成y=a(x-h)2+k的形式,并写出它们图象的开口方向、对称轴和顶点坐标.
(1)y=-x2+6x+1;
(2)y=2x2-3x+4.
(1)y=-x2+6x+1;
(2)y=2x2-3x+4.
考点:二次函数的三种形式
专题:计算题
分析:(1)先利用配方法得到顶点式y=-(x-3)2+10,然后根据二次函数的性质写出它们图象的开口方向、对称轴和顶点坐标.
(2)先利用配方法得到顶点式y=2(x-
)2-
,然后根据二次函数的性质写出它们图象的开口方向、对称轴和顶点坐标.
(2)先利用配方法得到顶点式y=2(x-
| 9 |
| 4 |
| 49 |
| 8 |
解答:解:(1)y=-(x-3)2+10,
二次函数图象的开口向下,对称轴为直线x=3,顶点坐标为(3,10);
(2)y=2(x-
)2-
,
二次函数图象的开口向上,对称轴为直线x=
,顶点坐标为(
,-
).
二次函数图象的开口向下,对称轴为直线x=3,顶点坐标为(3,10);
(2)y=2(x-
| 9 |
| 4 |
| 49 |
| 8 |
二次函数图象的开口向上,对称轴为直线x=
| 9 |
| 4 |
| 9 |
| 4 |
| 49 |
| 8 |
点评:本题考查了二次函数的三种形式:一般式:y=ax2+bx+c(a,b,c是常数,a≠0),该形式的优势是能直接根据解析式知道抛物线与y轴的交点坐标是(0,c);顶点式:y=a(x-h)2+k(a,h,k是常数,a≠0),其中(h,k)为顶点坐标,该形式的优势是能直接根据解析式得到抛物线的顶点坐标为(h,k);交点式:y=a(x-x1)(x-x2)(a,b,c是常数,a≠0),该形式的优势是能直接根据解析式得到抛物线与x轴的两个交点坐标(x1,0),(x2,0).

练习册系列答案
 举一反三单元同步过关卷系列答案
举一反三单元同步过关卷系列答案
相关题目
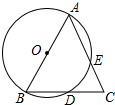 在△ABC中,AB=AC,以AB为直径的圆O分别交BC、AC于点D、E,
在△ABC中,AB=AC,以AB为直径的圆O分别交BC、AC于点D、E,