题目内容
1.甲口袋中装有两个相同的小球,它们分别写有数字1和2;乙口袋中装有三个相同的小球,它们分别写有数字3、4和5;两口袋中装有两个相同的小球,分别写有数字6和7,现从这三个口袋中各随机地取出1个小球,根据画树状图或列表的方法解答下列问题:(1)求取出的3个小球恰好有两个偶数的概率;
(2)求取出的3个小球全是奇数的概率.
分析 (1)画树状图得出所有等可能的情况数,找出取出的3个小球上恰好有两个偶数的情况数,即可求出所求概率;
(2)找出取出的3个小球上全是奇数的情况数,即可求出所求的概率.
解答 解:画树状图如下:
所有等可能的情况有12种,
(1)取出的3个小球上恰好有两个偶数的情况数有4种,即1,4,6;2,3,6;2,4,7;2,5,6,
则P(两个偶数)=$\frac{4}{12}$=$\frac{1}{3}$;
(2)取出的3个小球上全是奇数的情况数有2种,即1,3,7;1,5,7,
则P(三个奇数)=$\frac{2}{12}$=$\frac{1}{6}$.
点评 此题考查的是用列表法或树状图法求概率.列表法可以不重复不遗漏的列出所有可能的结果,适合于两步完成的事件;树状图法适合两步或两步以上完成的事件;解题时要注意此题是放回实验还是不放回实验.用到的知识点为:概率=所求情况数与总情况数之比.

练习册系列答案
相关题目
9.二元一次方程组$\left\{\begin{array}{l}{2x+y=10}\\{x=2y}\end{array}\right.$的解是( )
| A. | $\left\{\begin{array}{l}{x=4}\\{y=3}\end{array}\right.$ | B. | $\left\{\begin{array}{l}{x=6}\\{y=3}\end{array}\right.$ | C. | $\left\{\begin{array}{l}{x=4}\\{y=2}\end{array}\right.$ | D. | $\left\{\begin{array}{l}{x=2}\\{y=4}\end{array}\right.$ |
6.股民张智慧上星期五买进某公司1000股,每股27元,下表为本周每日该股票的涨跌情况.(单位:元)
(1)星期四收盘时,每股是多少元?
(2)本周内最高价是每股多少元?最低价是多少元?
(3)已知张智慧买进时付了0.15%的手续费,卖出时须付成交额0.15%的手续费和0.1%的交易税,如果张智慧在星期五收盘前将全部股票卖出,他的收益情况如何?
| 星期 | 一 | 二 | 三 | 四 | 五 |
| 每股涨跌 | +4 | +4.5 | -1 | -2.5 | -4 |
(2)本周内最高价是每股多少元?最低价是多少元?
(3)已知张智慧买进时付了0.15%的手续费,卖出时须付成交额0.15%的手续费和0.1%的交易税,如果张智慧在星期五收盘前将全部股票卖出,他的收益情况如何?
13.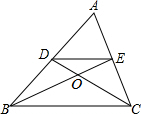 如图,在△ABC中两条中线BE、CD相交于点O,记△DOE的面积为S1,△COB的面积为S2,则S1:S2=( )
如图,在△ABC中两条中线BE、CD相交于点O,记△DOE的面积为S1,△COB的面积为S2,则S1:S2=( )
 如图,在△ABC中两条中线BE、CD相交于点O,记△DOE的面积为S1,△COB的面积为S2,则S1:S2=( )
如图,在△ABC中两条中线BE、CD相交于点O,记△DOE的面积为S1,△COB的面积为S2,则S1:S2=( )| A. | 1:4 | B. | 2:3 | C. | 1:3 | D. | 1:2 |
 如图,已知平面上有四个点A,B,C,D.
如图,已知平面上有四个点A,B,C,D.