题目内容
10.甲乙两地相距120千米,一辆汽车和一辆摩托车从两地同时出发相向而行,1.2小时相遇.相遇后,摩托车继续前进,汽车在相遇处停留10分钟后原速返回,结果在第一次相遇后半小时再次遇到摩托车,问汽车、摩托车每小时各行驶多少千米?分析 设汽车每小时行驶x千米,摩托车每小时行驶y千米,根据路程=速度×时间,即可得出关于x、y的二元一次方程组,解之即可得出结论.
解答 解:设汽车每小时行驶x千米,摩托车每小时行驶y千米,
根据题意得:$\left\{\begin{array}{l}{1.2(x+y)=120}\\{(\frac{1}{2}-\frac{10}{60})x=\frac{1}{2}y}\end{array}\right.$,
解得:$\left\{\begin{array}{l}x=60\\ y=40\end{array}\right.$.
答:汽车每小时行驶60千米,摩托车每小时行驶40千米.
点评 本题考查了二元一次方程组的应用,根据路程=速度×时间,列出关于x、y的二元一次方程组是解题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
20.下列运算中,正确的是( )
| A. | $\sqrt{9}$=±3 | B. | $\root{3}{-8}$=2 | C. | ±$\sqrt{9}$=3 | D. | ${(\root{3}{-8})}^{2}$=4 |
2.下列图形中∠1与∠2不是同位角的是( )
| A. |  | B. |  | C. |  | D. |  |
19. 如图:∠1与∠2互补,需要具备的条件是( )
如图:∠1与∠2互补,需要具备的条件是( )
 如图:∠1与∠2互补,需要具备的条件是( )
如图:∠1与∠2互补,需要具备的条件是( )| A. | ∠1=∠3 | B. | ∠3+∠4=180° | C. | ∠3=∠4 | D. | ∠3+∠4=90° |
 如图,已知AE∥BD,∠1=120°,∠2=32°,求∠C的度数.
如图,已知AE∥BD,∠1=120°,∠2=32°,求∠C的度数.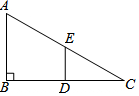 已知△ABC中,∠B=90°,D、E分别是BC、AC的中点,AB=4,BC=8,当△CDE绕点C旋转到A,E、D在同一直线上,求线段AE的长.
已知△ABC中,∠B=90°,D、E分别是BC、AC的中点,AB=4,BC=8,当△CDE绕点C旋转到A,E、D在同一直线上,求线段AE的长.