题目内容
(本题满分12分, 第(1)小题4分,第(2)小题4分,第(3)小题4分)
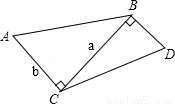
如图,已知等腰梯形ABCD中,AD∥BC,AD=1,BC=3,AB=CD=2,点E在BC边上,AE与BD交于点F,∠BAE=∠DBC,

(1)求证:△ABE∽△BCD;
(2)求tan∠DBC的值;
(3)求线段BF的长.
(1) (2)
(2) (3)
(3)
【解析】
试题分析:(1)根据等腰梯形的性质可得∠ABC=∠C,又∠BAE=∠DBC,可证△ABE∽△BCD;(2)过D作DG⊥BC,根据等腰梯形的性质求出BG,DG的长即可;(3)由△ABE∽△BCD可求出BE的长,在Rt△BDG中可求BD的长,然后利用 可求出BF的长.
可求出BF的长.
试题解析:(1)因为梯形ABCD是等腰梯形,所以∠ABC=∠C,又∠BAE=∠DBC,所以△ABE∽△BCD;(2)过D作DG⊥BC,如图:则CG= ,所以
,所以 , BG=2,所以
, BG=2,所以 ;(3) 因为△ABE∽△BCD,所以
;(3) 因为△ABE∽△BCD,所以 ,所以
,所以 所以BE
所以BE ,又
,又 , 因为AD∥BC,所以
, 因为AD∥BC,所以 ,所以
,所以 ,所以
,所以 .
.

考点:1. 等腰梯形的性质;2.相似三角形的判定与性质;3.勾股定理;4. 平行线分线段成比例定理.

练习册系列答案
相关题目
 ,点A的坐标为(0,1),则点E的坐标是 .
,点A的坐标为(0,1),则点E的坐标是 .
 向左平移2个单位,所得抛物线的表达式为( )
向左平移2个单位,所得抛物线的表达式为( ) ; B.
; B.  ;C.
;C.  ; D.
; D.  ;
; C.
C.  ∶1 D. 2∶1
∶1 D. 2∶1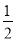 B. y轴 C.直线x=2 D.直线x=-
B. y轴 C.直线x=2 D.直线x=-
 ,
, .那么m与n满足的关系式是:m= (用含n的代数式表示m).
.那么m与n满足的关系式是:m= (用含n的代数式表示m).