题目内容
(7分)如图,已知∠ACB=∠CBD=90°,AC=b,CB=a,当BD与a,b之间满足怎样的关系时,△ACB∽△CBD?
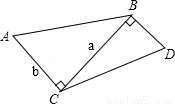
当BD= 时,△ACB∽△CBD.
时,△ACB∽△CBD.
【解析】
试题分析:要想证明△ACB∽△CBD,由于已知∠ACB=∠CBD=90°,所以只需要这两个角的夹边对应成比例即可,也就是 ,由此可得解.
,由此可得解.
试题解析:∵∠ACB=∠CBD=90°,
∴当 时,即当
时,即当 时,△ACB∽△CBD,
时,△ACB∽△CBD,
∴BD= .
.
因此当BD= 时,△ACB∽△CBD.
时,△ACB∽△CBD.
考点:相似三角形的判定与性质.

练习册系列答案
 第1卷单元月考期中期末系列答案
第1卷单元月考期中期末系列答案
相关题目
 是面积为
是面积为 的△
的△ 的重心,那么△
的重心,那么△ 的面积等于 ;
的面积等于 ;

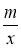 的图象的两个交点;
的图象的两个交点;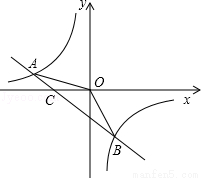
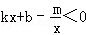 的解集(请直接写出答案).
的解集(请直接写出答案).

 B.
B.  C.
C.  D.
D.