题目内容

5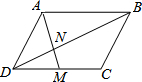．如图，在平行四边形ABCD中，如果点M为CD的中点，AM与BD相交于点N，若已知S△DMN=3，那么S△BAN等于（　　）
A．6B．9C．12D．3

分析 根据平行四边形性质及相似三角形的判定可得到相似三角形，根据面积比等于相似比的平方不难求得各面积的比．

解答 解：在?ABCD中，∵DC∥AB，AB=CD，
∵点M为CD的中点，
∴AB=2DM，
∴△DMN∽△BAN
∴DN：NB=DM：AB=1：2
∴S△DMN：S△ANB=（$\frac{DM}{AB}$）2=1：4，
∵S△DMN=3，
∴S△BAN=12，
故选，C．

点评 本题考查了平行四边形的性质，相似三角形的判定与性质，熟记各性质是解题的关键．

练习册系列答案
相关题目
15．若|a+2|=a+2，则a的取值范围是（　　）
A．a≥-2B．a≤-2C．a＜-2D．a＞-2
16．如图，AB是⊙O的直径，弦CD⊥AB于点C，点F是CD上一点，且满足$\frac{CF}{FD}$=$\frac{1}{3}$，连接AF并延长交⊙O于点E，连接AD、DE，若CF=2．AF=3．给出下列结论：
①△ADF∽△AED；②FG=3；③tan∠E=$\frac{\sqrt{5}}{2}$；④S△DAF=6$\sqrt{5}$．
其中正确结论的个数的是（　　）
A．1个B．2个C．3个D．4个
13．综合与实践：
问题情景：已知等腰Rt△ABC和等腰Rt△AED，∠AED=∠ACB=90°，点M，N分别是DB，EC的中点，连接MN．
问题：
（1）如图1，当点E在AB上，且点C和点D恰好重合时，探索MN与EC的数量关系，并加以证明；
（2）如图2，当点D在AB上，点E在△ABC外部时，（1）中的结论还成立吗？若成立，请给予证明，若不成立，请说明理由．
拓展探究：
（3）如图3，将图2中的等腰Rt△AED绕点A逆时针旋转n°（0＜n＜90），请猜想MN与EC的位置关系和数量关系．（不必证明）
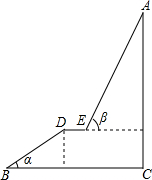20．如图，A为某旅游景区的最佳观景点，游客可从B处乘坐缆车先到达小观景平台DE观景，然后再由E处继续乘坐缆车到达A处，返程时从A处乘坐升降电梯直接到达C处，已知：AC⊥BC于C，DE∥BC，AC=200.4米，BD=100米，∠α=30°，∠β=70°，则AE的长度约为160米．（参考数据：sin70≈0.94，cos70°≈0.34，tan70°≈2.25）．
10．实数-$\sqrt{2}$的相反数是（　　）
A．-$\sqrt{2}$B．$\sqrt{2}$C．-$\frac{1}{\sqrt{2}}$D．$\frac{1}{\sqrt{2}}$
17．已知sinα=$\frac{\sqrt{3}}{2}$，则锐角α的度数是（　　）
A．30°B．37°C．45°D．60°
14．某校八年级学生小丽、小强和小红到某超市参加了社会实践活动，在活动中他们参与了某种水果的销售工作，已知该水果的进价为8元/千克，下面是他们在活动结束后的对话．
小丽：如果以10元/千克的价格销售，那么每天可售出300千克．
小强：如果以13元/千克的价格销售，那么每天可获取利润750元．
小红：通过调查验证，我发现每天的销售量y（千克）与销售单价x（元）（x＞8）之间存在一次函数关系．
（1）求y（千克）与x（元）（x＞8）的函数关系式；
（2）当销售单价为何值时，该超市销售这种水果每天获取的利润达到600元？[利润=销售量×（销售单价-进价）]
（3）一段时间后，发现这种水果每天的销售量均不低于225千克．则此时该超市销售这种水果每天获取的最大利润是多少？
15．已知两圆的半径分别为2和3，圆心距为5，则这两圆的位置关系是（　　）
A．外离B．外切C．相交D．内切

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网