题目内容
已知抛物线y=ax2-(3a+1)x+2(a+1),(a≠0).
(1)求证:无论a为任何非零实数,该抛物线与x轴都有交点;
(2)若抛物线y=ax2-(3a+1)x+2(a+1)与x轴交于A(m,0)、B(n,0)两点,m、n、a均为整数,一次函数y=kx+b(k≠0)的图象经过点P(n-1,n+1)、Q(0,a),求一次函数的表达式.
(1)求证:无论a为任何非零实数,该抛物线与x轴都有交点;
(2)若抛物线y=ax2-(3a+1)x+2(a+1)与x轴交于A(m,0)、B(n,0)两点,m、n、a均为整数,一次函数y=kx+b(k≠0)的图象经过点P(n-1,n+1)、Q(0,a),求一次函数的表达式.
考点:抛物线与x轴的交点,待定系数法求一次函数解析式
专题:
分析:(1)依据根的判别式即可判定;
(2)把点A(m,0)、B(n,0)代入抛物线y=ax2-(3a+1)x+2(a+1),解得关于x的方程的解;再进一步m、n、a为整数,探讨得出a的值,进一步确定m、n的数值,求得P、Q两点坐标,利用待定系数法求得问题即可.
(2)把点A(m,0)、B(n,0)代入抛物线y=ax2-(3a+1)x+2(a+1),解得关于x的方程的解;再进一步m、n、a为整数,探讨得出a的值,进一步确定m、n的数值,求得P、Q两点坐标,利用待定系数法求得问题即可.
解答:(1)证明:∵△=[-(3a+1)]2-4a×2(a+1)
=a2-2a+1
=(a-1)2≥0
∴无论a为任何非零实数,该抛物线与x轴都有交点.…
(2)解:∵抛物线y=ax2-(3a+1)x+2(a+1)与x轴交于A(m,0)、B(n,0)两点,
∴a≠1.
令y=ax2-(3a+1)x+2(a+1),(a≠0)中y=0,
有:ax2-(3a+1)x+2(a+1)=0.
解得:x=2,x=1+
.
∵m、n、a均为整数,
∴a=-1,m=0,n=2或m=2,n=0.
∵一次函数y=kx+b(k≠0)的图象经过点P(n-l,n+l)、Q(0,a),
∴当a=-1,n=2时,有P(1,3)、Q(0,-1),
解得:y=4x-1.
当a=-1,n=0时,有P(-1,1)、Q(0,-1),
解得:y=-2x-1.
=a2-2a+1
=(a-1)2≥0
∴无论a为任何非零实数,该抛物线与x轴都有交点.…
(2)解:∵抛物线y=ax2-(3a+1)x+2(a+1)与x轴交于A(m,0)、B(n,0)两点,
∴a≠1.
令y=ax2-(3a+1)x+2(a+1),(a≠0)中y=0,
有:ax2-(3a+1)x+2(a+1)=0.
解得:x=2,x=1+
| 1 |
| a |
∵m、n、a均为整数,
∴a=-1,m=0,n=2或m=2,n=0.
∵一次函数y=kx+b(k≠0)的图象经过点P(n-l,n+l)、Q(0,a),
∴当a=-1,n=2时,有P(1,3)、Q(0,-1),
解得:y=4x-1.
当a=-1,n=0时,有P(-1,1)、Q(0,-1),
解得:y=-2x-1.
点评:此题考查二次函数的实际运用,抛物线与x轴交点的问题,以及分类讨论思想的渗透.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
8的立方根与4的平方根之和是( )
| A、0 | B、4 | C、0或4 | D、0或-4 |
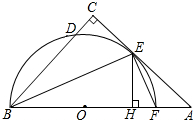 如图,在△ABC中,∠C=90°,∠ABC的平分线交AC于点E,过点E作BE的垂线交AB于点F,⊙O是△BEF的外接圆.
如图,在△ABC中,∠C=90°,∠ABC的平分线交AC于点E,过点E作BE的垂线交AB于点F,⊙O是△BEF的外接圆.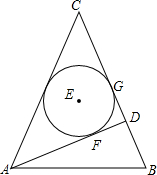 如图,在等腰△ABC中,CA=CB,AD是腰BC边上的高,△ACD的内切圆⊙E分别与边AD、BC相切于点F、G,连AE、BE.
如图,在等腰△ABC中,CA=CB,AD是腰BC边上的高,△ACD的内切圆⊙E分别与边AD、BC相切于点F、G,连AE、BE.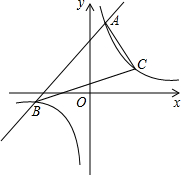 已知一次函数y1=x+m的图象与反比例函数
已知一次函数y1=x+m的图象与反比例函数