题目内容
17.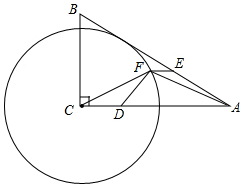 如图,在Rt△ABC中,∠A=30°,AC=8,以C为圆心,4为半径作⊙C.
如图,在Rt△ABC中,∠A=30°,AC=8,以C为圆心,4为半径作⊙C.(1)试判断⊙C与AB的位置关系,并说明理由;
(2)点F是⊙C上一动点,点D在AC上且CD=2,试说明△FCD~△ACF;
(3)点E是AB边上任意一点,在(2)的情况下,试求出EF+$\frac{1}{2}$FA的最小值.
分析 (1)结论:相切.作CM⊥AB于M.,只要证明CM=4,即可解决问题;
(2)由CF=4,CD=2,CA=8,推出CF2=CD•CA,推出$\frac{CF}{CD}$=$\frac{CA}{CF}$,由∠FCD=∠ACF,即可推出△FCD∽△ACF;
(3)作AE′⊥AB于E′,交⊙C于F′.由△FCD∽△ACF,可得$\frac{DF}{AF}$=$\frac{CF}{CA}$=$\frac{1}{2}$,推出DF=$\frac{1}{2}$AC,推出EF+$\frac{1}{2}$AF=EF+DF,所以欲求EF+$\frac{1}{2}$AF的最小值,就是要求EF+DF的最小值;
解答 (1)解:结论:相切.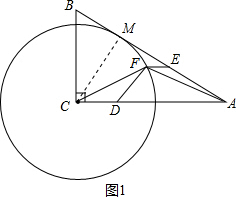
理由:作CM⊥AB于M.
在Rt△ACM中,∵∠AMC=90°,∠CAM=30°,AC=8,
∴CM=$\frac{1}{2}$AC=4,
∵⊙O的半径为4,
∴CM=r,
∴AB是⊙C的切线.
(2)证明: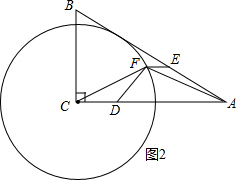
∵CF=4,CD=2,CA=8,
∴CF2=CD•CA,
∴$\frac{CF}{CD}$=$\frac{CA}{CF}$,∵∠FCD=∠ACF,
∴△FCD∽△ACF.
(3)解:作AE′⊥AB于E′,交⊙C于F′.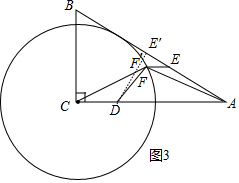
∵△FCD∽△ACF,
∴$\frac{DF}{AF}$=$\frac{CF}{CA}$=$\frac{1}{2}$,
∴DF=$\frac{1}{2}$AC,
∴EF+$\frac{1}{2}$AF=EF+DF,
∴欲求EF+$\frac{1}{2}$AF的最小值,就是要求EF+DF的最小值,
当E与E′,F与F′重合时,EF+DF的值最小,最小值=DE′=$\frac{1}{2}$AD=3.
点评 本题考查圆综合题、切线的判定和性质、相似三角形的判定和性质,垂线段最短等知识,解题的关键是学会添加常用辅助线,正确切线的证明方法,学会正确寻找相似三角形解决问题,学会利用垂线段最短解决问题,属于中考压轴题.

 孟建平小学滚动测试系列答案
孟建平小学滚动测试系列答案 黄冈天天练口算题卡系列答案
黄冈天天练口算题卡系列答案| 视力情况 | 0.7以下 | 0.7 | 0.8 | 0.9 | 1.0 | 1.0以上 |
| 人数所占的百分比 | 5% | 8% | 15% | 20% | 40% | 12% |
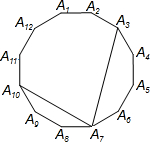 如图,正十二边形A1A2…A12,连接A3A7,A7A10,则∠A3A7A10的度数为( )
如图,正十二边形A1A2…A12,连接A3A7,A7A10,则∠A3A7A10的度数为( )| A. | 60° | B. | 65° | C. | 70° | D. | 75° |
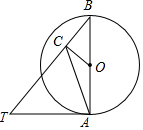 如图,AB是⊙O的直径,∠ABT=45°,AT=AB.
如图,AB是⊙O的直径,∠ABT=45°,AT=AB.
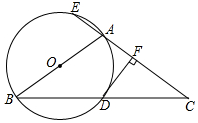 如图,△ABC中,AB=AC,以AB为直径的⊙O与BC相交于点D,与CA的延长线相交于点E,过点D作DF⊥AC于点F.
如图,△ABC中,AB=AC,以AB为直径的⊙O与BC相交于点D,与CA的延长线相交于点E,过点D作DF⊥AC于点F.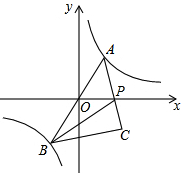 如图,反比例函数y=$\frac{k}{x}$的图象经过点(-$\sqrt{2}$,-4),点A是该图象第一象限分支上的动点,连结AO并延长交另一分支于点B,以AB为斜边作等腰直角三角形ABC,顶点C在第四象限,AC与x轴交于点P,连结BP.在点A运动过程中,当BP平分∠ABC时,点C的坐标是(2$\sqrt{2}$,-2).
如图,反比例函数y=$\frac{k}{x}$的图象经过点(-$\sqrt{2}$,-4),点A是该图象第一象限分支上的动点,连结AO并延长交另一分支于点B,以AB为斜边作等腰直角三角形ABC,顶点C在第四象限,AC与x轴交于点P,连结BP.在点A运动过程中,当BP平分∠ABC时,点C的坐标是(2$\sqrt{2}$,-2).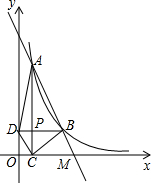 如图,直线AB经过x轴上的点M,与反比例函数y=$\frac{k}{x}$(x>0)的图象相交于点A(1,8)和B(m,n),其中m>1,AC⊥x轴于点C,BD⊥y轴于点D,AC与BD交于点P.
如图,直线AB经过x轴上的点M,与反比例函数y=$\frac{k}{x}$(x>0)的图象相交于点A(1,8)和B(m,n),其中m>1,AC⊥x轴于点C,BD⊥y轴于点D,AC与BD交于点P.