题目内容
20．过m边形的顶点能作7条对角线，n边形没有对角线，k边形有k条对角线，则（m-k）n=125．分析 若过m边形的一个顶点有7条对角线，则m=10；n边形没有对角线，只有三角形没有对角线，因而n=3；k边形有k条对角线，即得到方程$\frac{1}{2}$k（k-3）=k，解得k=5；正h边形的内角和与外角和相等，内角和与外角和相等的只有四边形，因而h=4．代入解析式就可以求出代数式的值．
解答 ：∵n边形从一个顶点发出的对角线有n-3条，
∴m=7+3=10，n=3，k=5，h=4；
∴（m-k）n=（10-5）3=125，
故答案为：125．
点评 本题考查了多边形的对角线，解决本题的关键是熟记n边形从一个顶点发出的对角线有n-3条，共有对角线$\frac{1}{2}$n（n-3）条．
练习册系列答案
相关题目
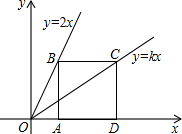如图，已知四边形ABCD是正方形，点B，C分别在两条直线y=2x和y=kx上，点A，D是x轴上两点．
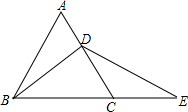如图所示，△ABC为等边三角形，BD为中线，延长BC至E，使 DE=BD．
如图，在图中求作⊙P，使得⊙P经过点M与点N，且圆心P到∠AOB两边的距离相等（要求：尺规作图，不写作法，保留作图痕迹，并把作图痕迹用黑色签字笔加黑）．
在一幅长80cm，宽50cm的矩形风景画的四周镶一条金色纸边，制成一幅矩形挂图，如果要使整个挂图的面积是ycm2，设金色纸边的宽为xcm，要求纸边的宽度不得少于1cm，同时不得超过2cm．
如图，一种某小区的两幢10层住宅楼间的距离为AC=30m，由地面向上依次为第1层、第2层、…、第10层，每层高度为3m．假设某一时刻甲楼在乙楼侧面的影长EC=h，太阳光线与水平线的夹角为α．