题目内容

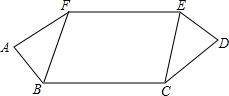已知：如图，AB=DE，AF=CD，EF=BC，∠A=∠D，求证：BF∥CE．
考点：全等三角形的判定与性质
专题：证明题
分析：在△AFB和△DCE中，证出△AFB≌△DCE，求出BF=EC，再根据EF=BC，证出四边形BFEC为平行四边形，从而得到BF∥CE．
解答：解：在△AFB和△DCE中，
AF=DC
∠A=∠D
AB=DE
，
则△AFB≌△DCE（SAS），
故BF=EC，
又∵EF=BC，
∴四边形BFEC为平行四边形，
∴BF∥CE．
点评：本题考查了全等三角形的判定与性质、平行四边形的判定与性质，灵活运用是解题的关键．
练习册系列答案
相关题目
如图，在△ABC中，已知∠BAC=90°，AD⊥BC于D，E是AB上一点，AF⊥CE于F，AD交CE于G点，
（1）求证：AC2=CE•CF；
（2）若∠B=38°，求∠CFD的度数．
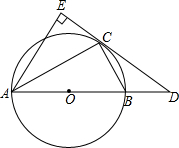如图，AB是⊙O的直径，D是AB的延长线上的一点，点C在⊙O上，AE⊥DC交
DC的延长线于点E，且AC平分∠EAB．
（1）求证：DE是⊙O的切线；
（2）若AE=8，AC=10，求⊙O的半径．
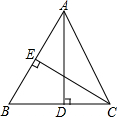如图，AD，CE是△ABC的高，已知AD=10，CE=9，AB=12，则BC=
 
．
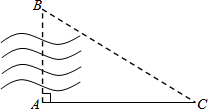如图，A、B两点在河两岸，为了测算这两点之间的距离，小华在河岸边选定一点C，测得AC=100米，∠A=90°，∠C=30°，则AB≈
 
米（精确到1米，参考数据：
2
≈1.41，
3
≈1.73）
已知：BE⊥CD，BE=DE，BC=DA，∠B=∠D．求证：
（1）△BEC≌△DAE；
（2）DF⊥BC．
⊙O中，AB是直径，弦CD与AB交于E，AE=8，BE=2，∠AEC=30°，求CD的长．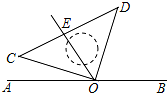
如图，一直角三角板COD的直角（∠COD=90°）顶点O落在直线AB上，射线OE平分∠AOD．
（1）如图，若∠AOC=20°，则∠BOD=
 
，∠COE=
 
．（直接写出结果）
（2）求
∠COE
∠BOD
．
（3）若∠COE=n∠AOC，则∠AOC=
 
．（直接写出结果，结果用含n的式子表示）
下列四组数中不能构成直角三角形的一组是（　　）
A、1，2，
5
B、
2
，2，
2
C、13，12，5
D、1，3，
7

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网