题目内容
11.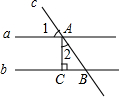 如图,直线c与直线a、b交于点A、B,且a∥b,线段AC垂直于直线b,垂足为点C.若∠1=55°,则∠2的度数是( )
如图,直线c与直线a、b交于点A、B,且a∥b,线段AC垂直于直线b,垂足为点C.若∠1=55°,则∠2的度数是( )| A. | 25° | B. | 35° | C. | 45° | D. | 55° |
分析 先根据平行线的性质求出∠ABC的度数,再由垂直的定义得出∠ACB的度数,根据三角形内角和定理即可得出结论.
解答 解:∵a∥b,∠1=55°,
∴∠ABC=55°.
∵AC⊥b,
∴∠ACB=90°,
∴∠2=90°-∠ABC=90°-55°=35°.
故选B.
点评 本题考查的是平行线的性质,用到的知识点为:两直线平行,同位角相等.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
1.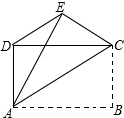 如图,已知四边形ABCD是矩形,把矩形沿直线AC折叠,点B落在点E处,连接DE,若DE:AC=3:5,则AD:AB的值为( )
如图,已知四边形ABCD是矩形,把矩形沿直线AC折叠,点B落在点E处,连接DE,若DE:AC=3:5,则AD:AB的值为( )
 如图,已知四边形ABCD是矩形,把矩形沿直线AC折叠,点B落在点E处,连接DE,若DE:AC=3:5,则AD:AB的值为( )
如图,已知四边形ABCD是矩形,把矩形沿直线AC折叠,点B落在点E处,连接DE,若DE:AC=3:5,则AD:AB的值为( )| A. | $\frac{1}{3}$ | B. | $\frac{1}{2}$ | C. | $\frac{3}{8}$ | D. | $\frac{3}{4}$ |
16.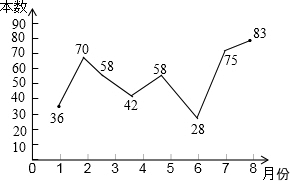 小明根据去年1~8月本班同学参加学校组织的“书香校园”活动中全班同学的课外阅读书籍的数量(单位:本),绘制了如图所示折线统计图,下列说法正确的是( )
小明根据去年1~8月本班同学参加学校组织的“书香校园”活动中全班同学的课外阅读书籍的数量(单位:本),绘制了如图所示折线统计图,下列说法正确的是( )
 小明根据去年1~8月本班同学参加学校组织的“书香校园”活动中全班同学的课外阅读书籍的数量(单位:本),绘制了如图所示折线统计图,下列说法正确的是( )
小明根据去年1~8月本班同学参加学校组织的“书香校园”活动中全班同学的课外阅读书籍的数量(单位:本),绘制了如图所示折线统计图,下列说法正确的是( )| A. | 阅读数量的平均数是57 | B. | 阅读数量的众数是42 | ||
| C. | 阅读数量的中位数是58 | D. | 有4个月的阅读数量超过60本 |
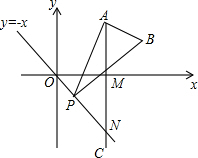 如图,已知点A的坐标为(3,3$\sqrt{3}$),AC⊥x轴于点M,交直线y=-x于点N,若点P是线段ON上的一个动点,∠APB=30°,BA⊥PA,若点P从点O出发,在线段ON上向点N运动时,B点也随之运动.
如图,已知点A的坐标为(3,3$\sqrt{3}$),AC⊥x轴于点M,交直线y=-x于点N,若点P是线段ON上的一个动点,∠APB=30°,BA⊥PA,若点P从点O出发,在线段ON上向点N运动时,B点也随之运动. 在一次手工制作中,小颖将长为16cm的铁丝首尾相接围成半径为4cm的扇形,则此扇形的面积为16cm2.
在一次手工制作中,小颖将长为16cm的铁丝首尾相接围成半径为4cm的扇形,则此扇形的面积为16cm2.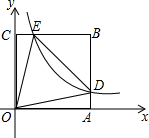 如图,已知反比例函数y=$\frac{k}{x}$(k>0)的图象与正方形OABC的边AB、BC分别交于点D、E.若正方形OABC的边长为1,△ODE是等边三角形,则k的值为2-$\sqrt{3}$.
如图,已知反比例函数y=$\frac{k}{x}$(k>0)的图象与正方形OABC的边AB、BC分别交于点D、E.若正方形OABC的边长为1,△ODE是等边三角形,则k的值为2-$\sqrt{3}$.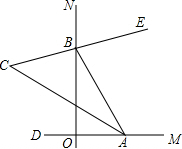 如图,∠MON=90°,点A,B分别在射线OM、ON上移动,BE是∠ABN的平分线,BE的反向延长线与∠OAB平分线相交于点C,试问:∠ACB的大小是否发生变化?如果保持不变,请给出证明;如果随点A、B移动发生变化,请求出变化范围.
如图,∠MON=90°,点A,B分别在射线OM、ON上移动,BE是∠ABN的平分线,BE的反向延长线与∠OAB平分线相交于点C,试问:∠ACB的大小是否发生变化?如果保持不变,请给出证明;如果随点A、B移动发生变化,请求出变化范围.