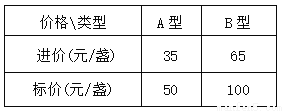
��Ŀ����
���������Ķ����Ķ�����һ�����֣�Ȼ��ش��������⣮
��֪ƽ��������M��x1��y1����N��x2��y2�������������ľ���������й�ʽ���㣺
MN=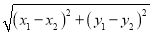 ��
��
���磺��֪P��3��1����Q��1����2�������������ľ���PQ=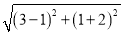 =
=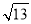 ��
��
��ֱ��Ӧ�á�
��1����֪A��2��-3����B��-4��5��������A��B�����ľ��룻
��2����֪��ABC�Ķ�������ֱ�ΪA��0��4����B����1��2����C��4��2���������ж���ABC����״����˵�����ɣ�
�����Ӧ�á�
��3����ͼ����ƽ��ֱ������ϵxOy�У����κ���y=x2��4��ͼ����x���ཻ������A��B������A�ڵ�B����ߣ�
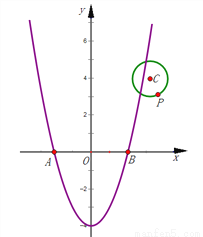
�����A��B�����ꣻ
�����P��m��n�����Ե�C��3��4��ΪԲ�ġ�1Ϊ�뾶��Բ��һ���㣬��PA2+PB2�����ֵ��
��1��AB=10�� ��2����ABC��ֱ�������Σ���3����A��-2,0��B��2,0������80. ����������������1�����������ľ��빫ʽ�����AB�ij�����2�����������ľ��빫ʽ�����AB��AC��BC�ij���Ȼ�����ݹ��ɶ������涨���ɶԡ�ABC����״�����жϣ���3������y=0�ã�x²-4=0�����x=2��x=-2���ʴ˿ɵõ�A��B�����ꣻ���������������ľ��빫ʽ��ʾ��PA²+PB²�ij���ͨ����...
��ϰ��ϵ�д�
�����Ŀ


 ��
�� ��������߳������ǣ� ����
��������߳������ǣ� ���� B.
B. 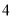 C.
C. 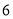 D.
D. 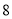
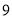 �ĸ���Ϊ�� ��
�ĸ���Ϊ�� ��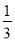 B.
B. 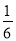 C.
C. 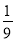 D.
D. 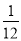
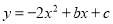 ��ͼ����A��0��2����B����1����4����
��ͼ����A��0��2����B����1����4����
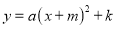 ����ʽ��
����ʽ��