题目内容
4. 一个正六边形和两个等边三角形的位置如图所示,∠3=70°,则∠1+∠2=50°.
一个正六边形和两个等边三角形的位置如图所示,∠3=70°,则∠1+∠2=50°.
分析 先根据正六边形及正三角形的性质用∠1表示出∠BAC,用∠2表示出∠ACB,用∠3表示出∠ABC,再由三角形内角和定理即可得出结论.
解答 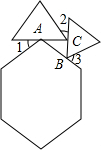 解:∵图中是一个正六边形和两个等边三角形,
解:∵图中是一个正六边形和两个等边三角形,
∴∠BAC=180°-∠1-120°=60°-∠1,∠ACB=180°-∠2-60°=120°-∠2,∠ABC=180°-60°-∠3=120°-∠3,
∵∠3=70°,
∴∠ABC=180°-60°-∠3=120°-70°=50°.
∵∠BAC+∠ACB+∠ABC=180°,即60°-∠1+120°-∠2+50°=180°,
∴∠1+∠2=50°.
故答案为:50°.
点评 本题考查的是三角形内角和定理,熟知三角形内角和是180°是解答此题的关键.

练习册系列答案
相关题目
19.某公司在销售一种产品进价为10元的产品时,每年总支出为10万元(不含进价).经过若干年销售得知,年销售量y(万件)是销售单价x(元)的一次函数,并得到如下部分数据:
(1)则y关于x的函数关系式是y=$-\frac{1}{2}x+13$;
(2)写出该公司销售这种产品的年利润w(万元)关于销售单价x(元)的函数关系式;当销售单价x为何值时,年利润最大?
(3)试通过(2)中的函数关系式及其大致图象,帮助该公司确定产品的销售单价范围,使年利润不低于14万元(请直接写出销售单价x的范围).
| 销售单价 x(元) | 16 | 18 | 20 | 22 |
| 年销售量y(万件) | 5 | 4 | 3 | 2 |
(2)写出该公司销售这种产品的年利润w(万元)关于销售单价x(元)的函数关系式;当销售单价x为何值时,年利润最大?
(3)试通过(2)中的函数关系式及其大致图象,帮助该公司确定产品的销售单价范围,使年利润不低于14万元(请直接写出销售单价x的范围).
13.如图是滨河公园中的两个物体,一天中四个不同时刻在太阳光的照射下落在地面上的影子,按照时间的先后顺序排列正确的是( )


| A. | (3)(4)(1)(2) | B. | (4)(3)(1)(2) | C. | (4)(3)(2)(1) | D. | (2)(4)(3)(1) |
14.下列几组数中不能作为直角三角形的三边长的是( )
| A. | $\sqrt{2}$,$\sqrt{2}$,2 | B. | 9,16,25 | C. | 6,8,10 | D. | 5,12,13 |
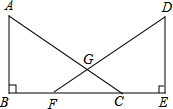 已知,如图,点B、F、C、E在同一直线上,AC、DF相交于点G,AB⊥BE,垂足为B,DE⊥BE,垂足为E,且AC=DF,BF=EC.求证:
已知,如图,点B、F、C、E在同一直线上,AC、DF相交于点G,AB⊥BE,垂足为B,DE⊥BE,垂足为E,且AC=DF,BF=EC.求证: 阅读与思考:整式乘法与因式分解是方向相反的变形,由(x+p)(x+q)=x2+(p+q)x+pq得,x2+(p+q)x+pq=(x+p)(x+q);利用这个式子可以将某些二次项系数是1的二次三项式分解因式,例如:将式子x2-x-6分解因式.这个式子的常数项-6=2×(-3),一次项系数-1=2+(-3),这个过程可用十字相乘的形式形象地表示:先分解常数项,分别写在十字交叉线的左上角和左下角;再分解常数项,分别写在十字交叉线的右上角和右下角;然后交叉相乘,求代数和,使其等于一次项系数.如图所示.这种分解二次三项式的方法叫“十字相乘法”,请同学们认真观察,分析理解后,解答下列问题.
阅读与思考:整式乘法与因式分解是方向相反的变形,由(x+p)(x+q)=x2+(p+q)x+pq得,x2+(p+q)x+pq=(x+p)(x+q);利用这个式子可以将某些二次项系数是1的二次三项式分解因式,例如:将式子x2-x-6分解因式.这个式子的常数项-6=2×(-3),一次项系数-1=2+(-3),这个过程可用十字相乘的形式形象地表示:先分解常数项,分别写在十字交叉线的左上角和左下角;再分解常数项,分别写在十字交叉线的右上角和右下角;然后交叉相乘,求代数和,使其等于一次项系数.如图所示.这种分解二次三项式的方法叫“十字相乘法”,请同学们认真观察,分析理解后,解答下列问题. 如图,Rt△ABC中,∠C=90°,沿DE折叠,使点A与点B重合.若BC=6,AC=8.
如图,Rt△ABC中,∠C=90°,沿DE折叠,使点A与点B重合.若BC=6,AC=8. 如图,C为线段AE上一动点(不与点A,E重合),在AE同侧分别作正三角形ABC和正三角形CDE,AD与BE交于点O,AD与BC交于点P,BE与CD交于点Q,连接PQ.以下五个结论:
如图,C为线段AE上一动点(不与点A,E重合),在AE同侧分别作正三角形ABC和正三角形CDE,AD与BE交于点O,AD与BC交于点P,BE与CD交于点Q,连接PQ.以下五个结论: