题目内容
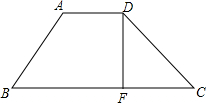 如图,在梯形ABCD中,AD∥BC,AB=CD,AD=5,BC=7,高DF=3,求腰长.
如图,在梯形ABCD中,AD∥BC,AB=CD,AD=5,BC=7,高DF=3,求腰长.考点:梯形,勾股定理,平行四边形的判定与性质
专题:
分析:过点D作DE∥AB交BC于点E,可证明四边形ABCD为平行四边形,进而得到CE长,再根据等腰三角形的性质可得CF=FE=
CE=1,再利用勾股定理计算出腰长即可.
| 1 |
| 2 |
解答: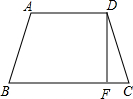 解:过点D作DE∥AB交BC于点E,
解:过点D作DE∥AB交BC于点E,
∵AD∥BC,
∴四边形ABCD为平行四边形,
∴AB=DE,AD=BE,
∵AD=5,BC=7,
∴CE=BC-AD=2,
∵AB=CD,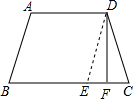
∴DE=DC,
∵DF为高,
∴CF=FE=
CE=1,
在Rt△DFC中,由勾股定理得:
DF2+FC2=DC2,
∴DC=
.
 解:过点D作DE∥AB交BC于点E,
解:过点D作DE∥AB交BC于点E,∵AD∥BC,
∴四边形ABCD为平行四边形,
∴AB=DE,AD=BE,
∵AD=5,BC=7,
∴CE=BC-AD=2,
∵AB=CD,

∴DE=DC,
∵DF为高,
∴CF=FE=
| 1 |
| 2 |
在Rt△DFC中,由勾股定理得:
DF2+FC2=DC2,
∴DC=
| 10 |
点评:此题主要考查了梯形,关键是掌握梯形中的辅助线的作法,作腰的平行线,可得平行四边形.

练习册系列答案
相关题目
下列分式中,计算正确的是( )
A、
| ||||||||||
B、
| ||||||||||
C、
| ||||||||||
D、
|
 画出函数y=-2x+2的图象,观察图象并回答下列问题.
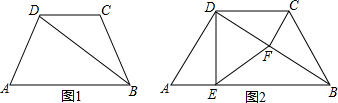
画出函数y=-2x+2的图象,观察图象并回答下列问题.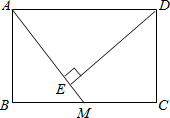 如图,在矩形ABCD中,AB=4,BC=6,M是BC的中点,DE⊥AM于点E.
如图,在矩形ABCD中,AB=4,BC=6,M是BC的中点,DE⊥AM于点E.