题目内容
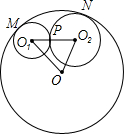 如图,⊙O1和⊙O2外切于P,并且⊙O和⊙O1、⊙O2分别内切于M、N,△O1O2O的周长为18cm.求⊙O的半径长.
如图,⊙O1和⊙O2外切于P,并且⊙O和⊙O1、⊙O2分别内切于M、N,△O1O2O的周长为18cm.求⊙O的半径长.考点:相切两圆的性质
专题:
分析:利用相切两圆的性质得出O1O2=r1+r2,O1O=R-r1,O2O=R-r2,进而求出即可.
解答:解:设⊙O、⊙O1和⊙O2的半径分别为R,r1,r2
∵⊙O1和⊙O2相外切
∴O1O2=r1+r2
又∵⊙O和⊙O1、⊙O2分别内切,
∴O1O=R-r1,O2O=R-r2,
∴△O1O2O的周长为18cm,即O1O2+OO1+OO2=(r1+r2)+(R-r1)+(R-r2)=18,
∴R=9(cm).
∵⊙O1和⊙O2相外切
∴O1O2=r1+r2
又∵⊙O和⊙O1、⊙O2分别内切,
∴O1O=R-r1,O2O=R-r2,
∴△O1O2O的周长为18cm,即O1O2+OO1+OO2=(r1+r2)+(R-r1)+(R-r2)=18,
∴R=9(cm).
点评:此题主要考查了相切两圆的性质,正确利用相切两圆圆心距和半径之间关系是解题关键.

练习册系列答案
相关题目
下列等式中是一元一次方程的是( )
| A、x2+x=6 | ||
| B、x-y=0 | ||
| C、x=0 | ||
D、
|
若(1+m)2+|n-3|=0,则(-m)n的值为( )
| A、1 | B、-1 | C、3 | D、-3 |
三门峡市大约有二百二十万人,将二百二十万用科学记数法表示为( )
| A、2.2×106 |
| B、2.2×105 |
| C、0.22×107 |
| D、22×105 |
 如图,已知⊙O1和⊙O2相交于点A、B,O1在⊙O2上,AC是⊙O1的直径,连接CB并延长,与⊙O2相交于点D,连结AD.
如图,已知⊙O1和⊙O2相交于点A、B,O1在⊙O2上,AC是⊙O1的直径,连接CB并延长,与⊙O2相交于点D,连结AD. 已知点P和点P′关于一条直线对称,请你画出这条对称轴.
已知点P和点P′关于一条直线对称,请你画出这条对称轴. 在如图所示的平面直角坐标系中,桥孔抛物线对应的二次函数关系式是y=-
在如图所示的平面直角坐标系中,桥孔抛物线对应的二次函数关系式是y=-