题目内容
19.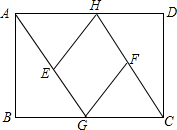 如图,在矩形ABCD中,H是AD上任意一点,AG∥CH交BC于点G,点E、F分别为AG、CH的中点,连接HE、FG.
如图,在矩形ABCD中,H是AD上任意一点,AG∥CH交BC于点G,点E、F分别为AG、CH的中点,连接HE、FG.(1)求证:四边形HEGF是平行四边形;
(2)当点G是BC的中点时,求证:四边形HEGF是菱形.
分析 (1)根据矩形的性质可得AH∥CG,再由AG∥CH可得四边形AGCH是平行四边形,进而可得AG=HC,从而可证出EG=HF,然后可得四边形HEGF是平行四边形;
(2)连接BE,证明△AEH≌△GEB,进而可得EB=EH,再根据直角三角形的性质可得BE=EG=$\frac{1}{2}$AG,从而可得EH=EG,可得结论四边形HEGF是菱形.
解答 证明:(1)∵四边形ABCD是矩形,
∴AH∥CG,
∵AG∥CH,
∴四边形AGCH是平行四边形,
∴AG=CH,
∵点E、F分别为AG、CH的中点,
∴FH=$\frac{1}{2}$CH,EG=$\frac{1}{2}$AG,
∴EG=HF,
∴四边形HEGF是平行四边形;
(2)连接BE,
∵G为BC中点,
∴BG=CG,
∵四边形HEGF是平行四边形,
∴AH=CG,
∴AH=BG,
∵AD∥BC,
∴∠DAG=∠AGB,
在△AEH和△GEB中,
$\left\{\begin{array}{l}{AE=EG}\\{∠HAE=∠BGE}\\{AH=BG}\end{array}\right.$,
∴△AEH≌△GEB(SAS),
∴EB=EH,
∵∠ABG=90°,E为AG中点,
∴BE=EG=$\frac{1}{2}$AG,
∴EH=EG,
∴四边形HEGF是菱形.
点评 此题主要考查了平行四边形和菱形的判定,关键是掌握一组对边平行且相等的四边形是平行四边形,一组邻边相等的平行四边形是菱形.

练习册系列答案
相关题目
9.若点(-1,2)在反比例函数y=$\frac{k}{x}$的图象上,则下列各点一定在该图象上的是( )
| A. | (-2,-1) | B. | (-$\frac{1}{2}$,2) | C. | (2,-1) | D. | ($\frac{1}{2}$,2) |
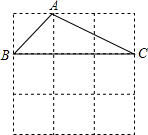 如图,△ABC的三个顶点分别在格子的3个交点上,请你试着再在格子的交点上找出三个点D,E,F,使得△DEF≌△ABC.
如图,△ABC的三个顶点分别在格子的3个交点上,请你试着再在格子的交点上找出三个点D,E,F,使得△DEF≌△ABC. 已知,如图,M是等腰三角形ABC底边BC上的中点,DM⊥AB,EF⊥AB,ME⊥AC,DG⊥AC,求证:四边形MEND是菱形.
已知,如图,M是等腰三角形ABC底边BC上的中点,DM⊥AB,EF⊥AB,ME⊥AC,DG⊥AC,求证:四边形MEND是菱形.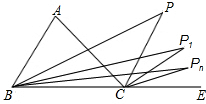 已知BP1平分∠ABC,CP1平分∠ACD;BP2平分∠P1BC,CP2平分∠P1CD;…,如此下去,得到∠Pn和∠A关系为∠Pn=($\frac{1}{2}$)n∠A.
已知BP1平分∠ABC,CP1平分∠ACD;BP2平分∠P1BC,CP2平分∠P1CD;…,如此下去,得到∠Pn和∠A关系为∠Pn=($\frac{1}{2}$)n∠A.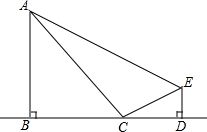 如图,分别过点A、E作AB⊥BD,ED⊥BD,C为线段BD上一动点,连接AC、EC.已知AB=9,DE=1,AE=17,设CD=x,用含x的代数式表示AC+CE.
如图,分别过点A、E作AB⊥BD,ED⊥BD,C为线段BD上一动点,连接AC、EC.已知AB=9,DE=1,AE=17,设CD=x,用含x的代数式表示AC+CE.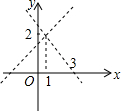 如图,不解关于x,y的方程组$\left\{\begin{array}{l}{y=x+1}\\{y=mx+n}\end{array}\right.$,请直接写出它的解$\left\{\begin{array}{l}{x=1}\\{y=2}\end{array}\right.$.
如图,不解关于x,y的方程组$\left\{\begin{array}{l}{y=x+1}\\{y=mx+n}\end{array}\right.$,请直接写出它的解$\left\{\begin{array}{l}{x=1}\\{y=2}\end{array}\right.$.