题目内容
1．
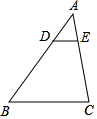如图，DE∥BC，分别交△ABC的边AB、AC于点D、E，$\frac{AD}{AB}$=$\frac{1}{3}$，若AE=1，则EC=（ ）| A． | 2 | B． | 3 | C． | 4 | D． | 6 |
分析 根据平行线分线段成比例定理得到$\frac{AD}{AB}$=$\frac{AE}{AC}$，即$\frac{1}{1+EC}$=$\frac{1}{3}$，然后利用比例性质求EC．
解答 解：∵DE∥BC，
∴$\frac{AD}{AB}$=$\frac{AE}{AC}$，即$\frac{1}{1+EC}$=$\frac{1}{3}$，
∴EC=2．
故选A．
点评 本题考查了平行线分线段成比例定理：三条平行线截两条直线，所得的对应线段成比例．推论：平行于三角形一边的直线截其他两边（或两边的延长线），所得的对应线段成比例．
练习册系列答案
相关题目
根据解答过程填空：
12．
有理数a、b在数轴上的位置如图，则下列各式不成立的是（ ）
有理数a、b在数轴上的位置如图，则下列各式不成立的是（ ）| A． | a+b＞0 | B． | a-b＞0 | C． | |b|＞a | D． | ab＜0 |
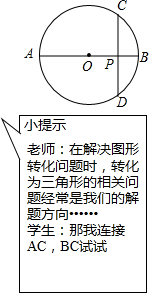如图，CD是圆O的弦，AB是直径，且CD⊥AB，垂足为P．
如图，在直角三角形ABC中，∠C=90°，AC=6，将三角形ABC沿CB向左平移得到三角形DEF，若平移的距离为3，则四边形DEBA的面积等于18．
已知：线段a，b