题目内容

20．在平面直角坐标系中，⊙A的半径为2，点A的坐标为（5，12），P（m，n）是⊙A上的一个动点，则m2+n2的最大值为225．

分析 确定m2+n2的最大值即OP的最大距离的平方，连接OA并延长与圆交于点P，此时OP最大，求出最大值即可．

解答 解：∵P（m，n），
OP=$\sqrt{{m}^{2}+{n}^{2}}$，
m2+n2的最大值即OP的最大距离的平方，
连接OA并延长与圆交于点P，此时OP最大，
∵点A的坐标为（5，12），
∴OA=13，又⊙A的半径为2，
∴OP=15，
m2+n2的最大值为225，
故答案为：225．

点评 本题考查的是坐标与图象的性质和点与圆的位置关系，确定OP取最大值时，点P的位置是解题的关键．

练习册系列答案
相关题目
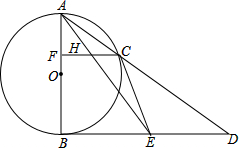6．如图，已知C是以AB为直径的圆O上一点，CF⊥AB于点F，直线AC与过点B的切线相交于点D，E为BD的中点，连接AE交CF于点H，连接CE．
（1）求证：点H是CF中点；
（2）求证：CH是⊙O的切线；
（3）若⊙O的半径为3，BE=4，求CF的长．
7．如果a、b、c的平均数是8，则a+3，b-6，c-12的平均数是3．
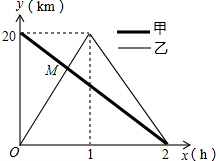8．在一条笔直的公路上有A、B两地，甲骑自行车从A地到B地；乙骑自行车从B地到A地，到达A地后立即按原路返回，如图是甲、乙两人离B地的距离y（km）与行驶时间x（h）之间的函数图象，根据图象解答以下问题：
（1）写出A、B两地的距离；
（2）分别求出甲离B地的距离y（km）与行驶时间x（h）的函数关系式；
（3）求出点M的坐标，并解释该点坐标所表示的实际意义．
15．在下列所给四个代数式中，选择合适的代数式并求值：①a+b；②a-b；③ab；④$\frac{a}{b}$．
（1）若a（a≠0）是关于x的方程x2+bx+a=0的根，我选a+b求值．
（2）若ab≠0且满足a2-7ab+12b2=0，我选$\frac{a}{b}$求值．
5．数学活动--求重叠部分的面积．
问题情境：数学活动课上，老师出示了一个问题：如图1，将两块全等的直角三角形纸片△ABC和△DEF叠放在一起，其中∠ACB=∠E=90°，BC=DE=6，AC=FE=8，顶点D与边AB的中点重合，DE经过点C，DF交AC于点C．求重叠部分（△DCG）的面积．
（1）独立思考：请解答老师提出的问题．
（2）合作交流：“希望”小组受此问题的启发，将△DEF绕点D旋转，使DE⊥AB交AC于点H，DF交AC于点G，如图2，求出重叠部分（△DGH）的面积，请写出解答过程．
（3）提出问题：老师要求各小组向“希望”小组学习，将△DEF绕点D旋转，再提出一个求重叠部分面积的问题．“爱心”小组提出的问题是：如图3，将△DEF绕点D旋转，DE，DF分别交AC于点M，N，使DM=MN，求重叠部分（△DMN）的面积．任务：请解决“爱心”小组所提出的问题，直接写出△DMN的面积是$\frac{75}{16}$．
12．阅读理解：
对于三个数a，b，c，用M{a，b，c}表示这三个数的平均数，用min{a，b，c}表示这三个数中最小的数．例如：M{-1，2.3}=$\frac{-1+2+3}{3}$=$\frac{4}{3}$； 
min{-1，2，3}=-1
min{-1，2，a}=$\left\{\begin{array}{l}{a（a≤-1）}\\{-1（a＞-1）}\end{array}\right.$
（1）填空：①M{（-2）3，（-3）2，（-$\frac{1}{4}$）-2}=$\frac{17}{3}$；②min{sin60°，cos45°，tan30°}=$\frac{1}{2}$；
③如果min{3，2x-5，-3x+24}=3，则x的取值范围为4≤x≤7．
探究归纳：
（2）①如果M{2015，x+2014，2x+2013}=min{2015，x+2014，2x+2013}，求x的值；
①根据①，你发现了结论“如果M{a，b，c}=min={a，b，c}，那么a=b=c（填a，b，c的大小关系）”．证明你发现的结论；
迁移运用：
③运用②的结论，填空：M{3x+y，x+2y+11，4x-y-2}=min{3x+y，x+2y+11，4x-y-2}，则x+y=-11．
9．4x-3是多项式4x2+5x+a的一个因式，那么a等于（　　）
A．-6B．6C．-9D．9
10．如图，已知EF∥CD，∠A=110°，∠EFC=35°，CF为∠ACD的平分线，那么AB与CD平行吗？说明理由．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网