题目内容
8. 在平面直角坐标系xOy中,抛物线y=2x2+mx+n经过点A(-1,a ),B(3,a),且最低点的纵坐标为-4.
在平面直角坐标系xOy中,抛物线y=2x2+mx+n经过点A(-1,a ),B(3,a),且最低点的纵坐标为-4.(1)求抛物线的表达式及a的值;
(2)设抛物线顶点C关于y轴的对称点为点D,点P是抛物线对称轴上一动点,记抛物线在点A,B之间的部分为图象G(包含A,B两点).如果直线DP与图象G恰有两个公共点,结合函数图象,求点P纵坐标t的取值范围.
分析 (1)根据点A、B的坐标可以得到对称轴方程为x=1,结合已知条件得到该抛物线的顶点坐标为(1,-4),则易求该抛物线的解析式;
(2)通过图象可以看出点B纵坐标t的取值范围.
解答 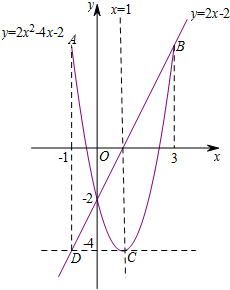 解:(1)∵抛物线y=2x2+mx+n过点A(-1,a ),B(3,a),
解:(1)∵抛物线y=2x2+mx+n过点A(-1,a ),B(3,a),
∴抛物线的对称轴x=1.
∵抛物线最低点的纵坐标为-4,
∴抛物线的顶点是(1,-4).
∴抛物线的表达式是y=2(x-1)2-4,
即y=2x2-4x-2.
把A(-1,a )代入抛物线表达式,求出a=4;
(2)∵抛物线顶点C(1,-4)关于y轴的对称点为点D,
∴D(-1,-4).
求出直线CD的表达式为y=-4.
求出直线BD的表达式为y=2x-2,当x=1时,y=0.
所以-4<t≤0.
点评 本题考查了待定系数法求二次函数解析式,二次函数图象与几何变换.需要学生具备画图的能力和识别图形的能力,要熟练掌握.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
13. 数轴上有A,B,C,D四个点,其中绝对值相等的点是( )
数轴上有A,B,C,D四个点,其中绝对值相等的点是( )
 数轴上有A,B,C,D四个点,其中绝对值相等的点是( )
数轴上有A,B,C,D四个点,其中绝对值相等的点是( )| A. | 点A与点D | B. | 点A与点C | C. | 点B与点C | D. | 点B与点D |
 如图,在?ABCD中,E是BC边上一点,试在AD边上找一点F,使四边形AECF是平行四边形,并说明理由.
如图,在?ABCD中,E是BC边上一点,试在AD边上找一点F,使四边形AECF是平行四边形,并说明理由.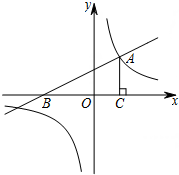 如图,一次函数y=$\frac{1}{2}$x+2的图象与x轴交于点B,与反比例函数y=$\frac{k}{x}$的图象的一个交点为A(2,m).
如图,一次函数y=$\frac{1}{2}$x+2的图象与x轴交于点B,与反比例函数y=$\frac{k}{x}$的图象的一个交点为A(2,m).