题目内容
13.x,y满足0<x<y,且$\sqrt{x}+\sqrt{y}=\sqrt{2000}$,则不同的整数对(x,y)的对数为( )| A. | 7 | B. | 8 | C. | 9 | D. | 10 |
分析 把已知等式右边化为最简二次根式后,分为两个二次根式相加的形式,由x与y不同,且0<x<y,确定出不同的整数对(x,y)的对数即可.
解答 解:∵0<x<y,且$\sqrt{x}$+$\sqrt{y}$=$\sqrt{2000}$=20$\sqrt{5}$=$\sqrt{5}$+19$\sqrt{5}$=2$\sqrt{5}$+18$\sqrt{5}$=3$\sqrt{5}$+17$\sqrt{5}$=4$\sqrt{5}$+16$\sqrt{5}$=5$\sqrt{5}$+15$\sqrt{5}$=6$\sqrt{5}$+14$\sqrt{5}$=7$\sqrt{5}$+13$\sqrt{5}$=8$\sqrt{5}$+12$\sqrt{5}$=9$\sqrt{5}$+11$\sqrt{5}$,
∴不同的整数对(x,y)的对数为9,
故选C
点评 此题考查了二次根式的化简求值,熟练掌握运算法则是解本题的关键.

练习册系列答案
相关题目
11.一元二次方程2x2+3x+1=0的根的情况是( )
| A. | 有两个不相等的实数根 | B. | 有两个相等的实数根 | ||
| C. | 没有实数根 | D. | 无法确定 |
4.在同一直线上,线段AB=4cm,线段BC=3cm,则线段AC=( )
| A. | 7cm | B. | 12cm | C. | 1cm | D. | 7cm或1cm |
18.在下列函数中,属于反比例函数的是( )
| A. | y=x-1 | B. | $y=\frac{8}{x^2}$ | C. | $y=\frac{-2}{x}$ | D. | $\frac{y}{x}=2$ |
5.已知点A(-2,y1)、B(-1,y2)、C(3,y3)都在反比例函数y=$\frac{3}{2x}$的图象上,则( )
| A. | y1<y2<y3 | B. | y3<y2<y1 | C. | y3<y1<y2 | D. | y2<y1<y3 |
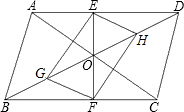 如图,平行四边形ABCD的对角线相交于点O,EF过点O,点G、H分别是OB、OD的中点,四边形EFGH是平行四边形吗?为什么?
如图,平行四边形ABCD的对角线相交于点O,EF过点O,点G、H分别是OB、OD的中点,四边形EFGH是平行四边形吗?为什么?