题目内容
13.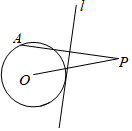 如图,⊙O的半径为4,点P是⊙O外的一点,PO=10,点A是⊙O上的一个动点,连接PA,直线l垂直平分PA,当直线l与⊙O相切时,PA的长度为$\frac{21}{2}$.
如图,⊙O的半径为4,点P是⊙O外的一点,PO=10,点A是⊙O上的一个动点,连接PA,直线l垂直平分PA,当直线l与⊙O相切时,PA的长度为$\frac{21}{2}$.
分析 如图设切点为E,作OF⊥PA于F,连接OE.直线l交PA于K,则四边形OEKF是矩形.设AK=PK=x,由OE=KF=4,推出AF=x-4,PF=x+4,由OF2=OA2-AF2=OP2-PF2,列出方程即可解决问题.
解答 解: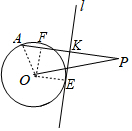 如图设切点为E,作OF⊥PA于F,连接OE.直线l交PA于K,则四边形OEKF是矩形.
如图设切点为E,作OF⊥PA于F,连接OE.直线l交PA于K,则四边形OEKF是矩形.
设AK=PK=x,
∵OE=KF=4,
∴AF=x-4,PF=x+4,
∵OF2=OA2-AF2=OP2-PF2,
∴42-(x-4)2=102-(x+4)2,
∴x=$\frac{21}{4}$,
∴PA=2x=$\frac{21}{2}$,
故答案为$\frac{21}{2}$.
点评 本题考查切线的性质、垂直平分线的性质、勾股定理、矩形的判定和性质等知识,解题的关键是学会添加常用辅助线,构造特殊四边形解决问题,属于中考常考题型.

练习册系列答案
相关题目
1.△ABC∽△DEF,且它们的周长之比为2:3,则它们的面积之比为( )
| A. | 2:3 | B. | 4:6 | C. | 4:9 | D. | 3:2 |
8.若1≤x≤3,则化简$\sqrt{{x}^{2}-2x+1}$+$\sqrt{{x}^{2}-6x+9}$的结果为( )
| A. | 2 | B. | 2x-4 | C. | 4-2x | D. | -2 |
18.既是方程2x-y=3的解,又是方程3x-4y=2的解的是( )
| A. | $\left\{\begin{array}{l}x=1\\ y=2\end{array}\right.$ | B. | $\left\{\begin{array}{l}x=2\\ y=1\end{array}\right.$ | C. | $\left\{\begin{array}{l}x=4\\ y=3\end{array}\right.$ | D. | $\left\{\begin{array}{l}x=-4\\ y=-5\end{array}\right.$ |
2.在平面直角坐标系中,已知A(-4,1),B(-1,-3),将线段AB向右平移得到线段A′B′,若A′坐标为(-2,1),则点B′在( )
| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
3.下列说法正确的是( )
| A. | 直线a、b都经过点m | B. | 直线AB、CD都经过点M | ||
| C. | 延长射线AB到C | D. | 线段、射线、直线中,线段最短 |
 如图,按角的位置关系填空:∠3与∠2是内错角;∠B 与∠3 是同旁内角.
如图,按角的位置关系填空:∠3与∠2是内错角;∠B 与∠3 是同旁内角.