题目内容
3.在?ABCD中,它的周长为32,∠ABC的角平分线交直线AD于点E,并且AE:DE=3:2,则AB=6或12.分析 分两种情形①当点E在相等AD上时,②当点E在AD的延长线上时,分别列出方程求出即可.
解答 解:如图所示①当点E在相等AD上时,
∵四边形ABCD是平行四边形,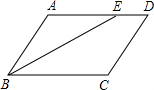
∴AD∥BC,AD=BC,AB=CD,
∴∠AEB=∠CBE,
∵BE是∠ABC的平分线,
∴∠ABE=∠CBE,
∴∠ABE=∠AEB,
∴AB=AE,
∵AE:ED=3:2,设AE=AB=3k,DE=2k
∵?ABCD的周长为32,
∴AB+AD=16,
∴3k+5k=16,
∴k=2,
∴AB=6,
②当点E在AD的延长线上时,
同理可证AB=AE=3k,DE=2k,
∵AB+AD=16,
∴3k+k=16,
∴k=4,
∴AB=12,
综上所述,AB的长为6或12.
故答案为6或12.
点评 本题考查平行四边形的性质.角平分线的定义、等腰三角形的判定和性质等知识,解题的关键是学会用分类讨论的思想思考问题,属于中考常考题型.

练习册系列答案
相关题目


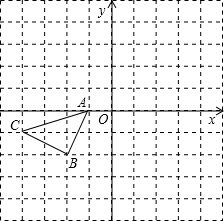 如图所示的正方形网格中,△ABC的顶点均在格点上,请在所给直角坐标系中按要求画图和解答下列问题:
如图所示的正方形网格中,△ABC的顶点均在格点上,请在所给直角坐标系中按要求画图和解答下列问题: 把两张等宽的矩形纸条交叉重叠在一起,
把两张等宽的矩形纸条交叉重叠在一起,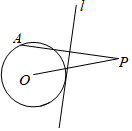 如图,⊙O的半径为4,点P是⊙O外的一点,PO=10,点A是⊙O上的一个动点,连接PA,直线l垂直平分PA,当直线l与⊙O相切时,PA的长度为$\frac{21}{2}$.
如图,⊙O的半径为4,点P是⊙O外的一点,PO=10,点A是⊙O上的一个动点,连接PA,直线l垂直平分PA,当直线l与⊙O相切时,PA的长度为$\frac{21}{2}$.