题目内容
1.已知正方形ABCD的边长为2cm,以CD为边所作的等腰直角三角形CDE的直角顶点为点E,则cos∠ABE=$\frac{\sqrt{2}}{2}$或$\frac{\sqrt{10}}{10}$.分析 如图所示,有两种情况:①点E在正方形ABCD的内部,利用正方形的性质得到点E是中心,则∠ABE=45°,易求cos∠ABE=$\frac{\sqrt{2}}{2}$;
②点E在正方形ABCD的外部,根据等腰直角三角形的性质和勾股定理以及解直角三角形进行解答.
解答 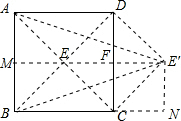 解:分两种情况:
解:分两种情况:
①点E在正方形ABCD的内部,利用正方形的性质得到点E是正方形ABCD的中心,则∠ABE=45°,
所以cos∠ABE=cos45°=$\frac{\sqrt{2}}{2}$;
②点E在正方形ABCD的外部.
如图,过点E′作E′N⊥BC延长线于点N,过点E′作E′M⊥AB于点M.∵△CDE是等腰直角三角形,
∴易求BM=E′N=$\frac{1}{2}$CD=1,E′F=$\frac{1}{2}$CD=1,
∴在直角△BME′中,由勾股定理得到:BE′=$\sqrt{B{M}^{2}+ME{′}^{2}}$=$\sqrt{{1}^{2}+{3}^{2}}$=$\sqrt{10}$,
∴cos∠ABE=$\frac{BM}{BE′}$=$\frac{1}{\sqrt{10}}$=$\frac{\sqrt{10}}{10}$.
综上所述,cos∠ABE=$\frac{\sqrt{2}}{2}$或cos∠ABE=$\frac{\sqrt{10}}{10}$.
故答案是:$\frac{\sqrt{2}}{2}$或$\frac{\sqrt{10}}{10}$.
点评 本题考查了解直角三角形,正方形的性质.解题时,要对点E位置进行分类讨论,以防漏解.

练习册系列答案
相关题目
11.下列实数中,属于无理数的是( )
| A. | -2 | B. | 0 | C. | $\sqrt{7}$ | D. | $\frac{1}{2}$ |
6.下列方程中,是一元一次方程的为( )
| A. | 2x-y=1 | B. | x2-y=2 | C. | $\frac{y}{2}$-2y=3 | D. | y2=4 |
13.下列各数:-(-2),-|-2|,(-2)2,-22,(-2)3,-23,负数个数为( )
| A. | 2个 | B. | 3个 | C. | 4个 | D. | 5个 |
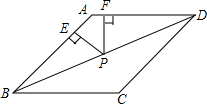 菱形ABCD中,点P为对角线BD上一动点,PE⊥AB于E,PF⊥AD于F,求证:PE+PF为定值.
菱形ABCD中,点P为对角线BD上一动点,PE⊥AB于E,PF⊥AD于F,求证:PE+PF为定值.