题目内容
求证:全等三角形对应边上的中线相等.(画出图形,写出已知、求证证明)
已知:
图形:
 .
.
求证:
证明:
已知:
如图,△ABC≌△A1B1C1,AD、A1D1分别是对应边BC、B1C1的中线
如图,△ABC≌△A1B1C1,AD、A1D1分别是对应边BC、B1C1的中线
.图形:


求证:
AD=A1D1
AD=A1D1
.证明:
∵△ABC≌△A1B1C1,
∴AB=A1B1,BC=B1C1,∠B=∠B1,
∵AD、A1D1分别是对应边BC、B1C1的中线,
∴BD=
BC,B1D1=
B1C1,
∴BD=B1D1,
在△ABD和△A1B1D1中
,
∴△ABD≌△A1B1D1(SAS),
∴AD=A1D1
∴AB=A1B1,BC=B1C1,∠B=∠B1,
∵AD、A1D1分别是对应边BC、B1C1的中线,
∴BD=
| 1 |
| 2 |
| 1 |
| 2 |
∴BD=B1D1,
在△ABD和△A1B1D1中
|
∴△ABD≌△A1B1D1(SAS),
∴AD=A1D1
∵△ABC≌△A1B1C1,
∴AB=A1B1,BC=B1C1,∠B=∠B1,
∵AD、A1D1分别是对应边BC、B1C1的中线,
∴BD=
BC,B1D1=
B1C1,
∴BD=B1D1,
在△ABD和△A1B1D1中
,
∴△ABD≌△A1B1D1(SAS),
∴AD=A1D1
.∴AB=A1B1,BC=B1C1,∠B=∠B1,
∵AD、A1D1分别是对应边BC、B1C1的中线,
∴BD=
| 1 |
| 2 |
| 1 |
| 2 |
∴BD=B1D1,
在△ABD和△A1B1D1中
|
∴△ABD≌△A1B1D1(SAS),
∴AD=A1D1
分析:首先根据△ABC≌△A1B1C1,可得AB=A1B1,BC=B1C1,∠B=∠B1,进而得到中线BD=B1D1,再证明△ABD≌△A1B1D1可得AD=A1D1.
解答: 已知:如图,△ABC≌△A1B1C1,AD、A1D1分别是对应边BC、B1C1的中线.
已知:如图,△ABC≌△A1B1C1,AD、A1D1分别是对应边BC、B1C1的中线.
求证:AD=A1D1.
证明:∵△ABC≌△A1B1C1,
∴AB=A1B1,BC=B1C1,∠B=∠B1,
∵AD、A1D1分别是对应边BC、B1C1的中线,
∴BD=
BC,B1D1=
B1C1,
∴BD=B1D1,
在△ABD和△A1B1D1中
,
∴△ABD≌△A1B1D1(SAS),
∴AD=A1D1.
 已知:如图,△ABC≌△A1B1C1,AD、A1D1分别是对应边BC、B1C1的中线.
已知:如图,△ABC≌△A1B1C1,AD、A1D1分别是对应边BC、B1C1的中线.求证:AD=A1D1.
证明:∵△ABC≌△A1B1C1,
∴AB=A1B1,BC=B1C1,∠B=∠B1,
∵AD、A1D1分别是对应边BC、B1C1的中线,
∴BD=
| 1 |
| 2 |
| 1 |
| 2 |
∴BD=B1D1,
在△ABD和△A1B1D1中
|
∴△ABD≌△A1B1D1(SAS),
∴AD=A1D1.
点评:此题主要考查学生对全等三角形的性质及判定的理解及运用能力.注意命题的证明的格式、步骤.

练习册系列答案
相关题目
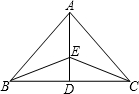 已知:如图,△ABC中,AB=AC,∠ABC、∠ACB的平分线交于点E,直线AE交BC于D.
已知:如图,△ABC中,AB=AC,∠ABC、∠ACB的平分线交于点E,直线AE交BC于D.