题目内容
抛物线y=ax2+bx+c(a≠0)的对称轴为直线x=1,且经过(﹣1,0)点(如图所示),康康依据图象写出了四个结论:
①如果点(﹣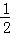 ,y1)和(2,y2)都在抛物线上,那么y1<y2;
,y1)和(2,y2)都在抛物线上,那么y1<y2;
②b2﹣4ac>0;
③m(am+b)<a+b(m≠1的实数);
④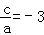 ;
;
康康所写结论正确的有__________(只填序号)
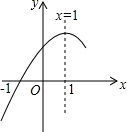
①②③④(只填序号)
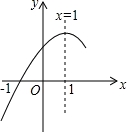
【考点】二次函数图象与系数的关系;二次函数图象上点的坐标特征.
【专题】探究型.
【分析】根据二次函数具有对称性,抛物线y=ax2+bx+c(a≠0)的对称轴为直线x=1,可知x=0和x=2时的函数值一样,由图象可以判断①;根据函数 图象与x轴的交点可判断②;根据函数开口向下,可知y=ax2+bx+c具有最大值,可判断③;根据抛物线y=ax2+bx+c(a≠0)的对称轴为直线x=1,且经过(﹣1,0)点,可知y=0时,x=2,从而可以判断④.
图象与x轴的交点可判断②;根据函数开口向下,可知y=ax2+bx+c具有最大值,可判断③;根据抛物线y=ax2+bx+c(a≠0)的对称轴为直线x=1,且经过(﹣1,0)点,可知y=0时,x=2,从而可以判断④.
【解答】解:∵抛物线y=ax2+bx+c(a≠0)的对称轴为直线x=1,
∴x=0与x=2时的函数值相等,由图象可知,x=0的函数值大于x=﹣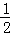 时的函数值.
时的函数值.
∴点(﹣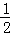 ,y1)和(2,y2)都在抛物线上,则y1<y2(故①正确).
,y1)和(2,y2)都在抛物线上,则y1<y2(故①正确).
∵x=0时,函数图象与x轴两个交点,
∴ax2+bx+c=0时,b2﹣4ac>0(故②正确).
∵由图象可知,x=1时,y=ax2+bx+c取得最大值,
∴当m≠1时,am2+bm+c<a+b+c.
即m(am+b)<a+b(m≠1的实数)(故③正确).
∵抛物线y=ax2+bx+c(a≠0)的对称轴为直线x=1,且经过(﹣1,0)点,
∴当y=0时,x的值为﹣1或3.
∴ax2+bx+c=0时的两根之积为: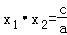 ,x1•x2=(﹣1)×3=﹣3.
,x1•x2=(﹣1)×3=﹣3.
∴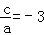 (故④正确).
(故④正确).
故答案为:①②③④.
【点评】本题考查二次函数图象与系数的关系,解题的关键是利用数形结合的思想将二次函数与函数图象结合在一起.

 轻松夺冠全能掌控卷系列答案
轻松夺冠全能掌控卷系列答案
 B.
B. C.
C. D.
D.
 :2 D.
:2 D.

 出一个代数恒等式是( )
出一个代数恒等式是( )