已知菱形ABCD的对角线AC.BD的长度是关于x的方程x2-13x+36=0的两个实数根.则此菱形的面积是( )A．18B．30C．36D．不确定题目和参考答案——青夏教育精英家教网—

题目内容

6．已知菱形ABCD的对角线AC，BD的长度是关于x的方程x²-13x+36=0的两个实数根，则此菱形的面积是（　　）

A．

B．

C．

D．

不确定

分析先利用因式分解法解方程得到AC和BD的长，然后根据菱形的面积公式求解．

解答解：x²-13x+36=0，
（x-9）（x-4）=0，
∴x-9=0或x-4=0，
∴x₁=9，x₂=4，
即菱形ABCD的对角线AC，BD的长度为9和4，
∴此菱形的面积=$\frac{1}{2}$×9×4=18．
故选A．

点评本题考查了解一元二次方程-因式分解法：先把方程的右边化为0，再把左边通过因式分解化为两个一次因式的积的形式，那么这两个因式的值就都有可能为0，这就能得到两个一元一次方程的解，这样也就把原方程进行了降次，把解一元二次方程转化为解一元一次方程的问题了（数学转化思想）．也考查了菱形的性质．

练习册系列答案

相关题目

16．

用四个完全一样的长方形（长、宽分别设为x、y）拼成如图所示的大正方形，已知大正方形的面积为36，中间空缺的小正方形的面积为4，则下列关系式中不正确的是（　　）

17．若2^x=3，2^y=5，则2^x+y=（　　）

14．

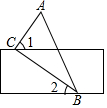如图，将直尺和直角三角板ABC按如图方式摆放，已知∠ACB=90°，∠1=65°，则∠2的大小是（　　）

1．

已知A、B两地相距80km，甲、乙两人沿同一条公路从A地到B地，乙骑自行车，甲骑摩托车，DE、OC分别表示甲、乙两人离开A地的距离（km）与乙出发的时间（h）的关系，根据图象填空：
（1）乙先出发1h后，甲才出发；
（2）大约在乙出发后1.5h，两人相遇，这时他们离A地20km；
（3）甲到达B地时，乙离开A地40km；
（4）甲的速度是40km/h；乙的速度是$\frac{40}{3}$km/h；
（5）甲离开A地的距离s（km）与乙出发的时间t（h）的关系式为s=40t-40（1≤t≤3）．

11．若函数y=-2mx-（m²-3）的图象经过点（0，1），且y随x的增大而增大．则m=-$\sqrt{3}$．

18．某校开展以“我最喜欢的职业”为主题的调查活动，通过对学生的随机抽样调查得到一组数据，如图是根据这组数据绘制的不完整的折线统计图和扇形统计图．
（1）在这次随机抽样调查中，共抽查了200名学生；
（2）把折线统计图补充完整；
（3）扇形统计图中，公务员部分对应的圆心角的度数72°；
（4）若从被调查的学生中任意抽取一名，求抽取的这名学生最喜欢的职业是“教师”的概率．

15．（1）如图（1），在Rt△ABC中，∠ACB=90°，∠B=60°，在图中作出∠ACB的三等分线CD，CE．（要求：尺规作图，保留作图痕迹，不写作法）
（2）由（1）知，我们可以用尺规作图作出直角的三等分线，但是仅仅使用尺规却不能把任意一个角分成三等分，为此，人们发明了许多等分角的机械器具，如图（2）是用三张硬纸片自制的一个最简单的三分角器，与半圆O相接的AB带的长度与半圆的半径相等；BD带的长度任意，它的一边与直线AC形成一个直角，且与半圆相切于点B，假设需要将∠KSM三等分，如图（3），首先将角的顶点S置于BD上，角的一边SK经过点A，另一边SM与半圆相切，连接SO，则SB，SO为∠KSM的三等分线，请你证明．

16．计算下列各式的值（精确到0.001）
（1）$\sqrt{7}$-$\sqrt{6}$+$\sqrt{5}$
（2）$\root{3}{9}$+$\sqrt{2}$-π
（3）|$\sqrt{3}$-2|+2$\sqrt{3}$．

试题分类