题目内容
18.若矩形的长和宽是方程x2-7x+12=0的两根,则矩形的对角线之和为( )| A. | 5 | B. | 7 | C. | 8 | D. | 10 |
分析 设矩形的长和宽分别为a、b,根据根与系数的关系得到a+b=7,ab=12,利用勾股定理得到矩形的对角线长=$\sqrt{{a}^{2}+{b}^{2}}$,再利用完全平方公式和整体代入的方法可计算出矩形的对角线长为5,则根据矩形的性质得到矩形的对角线之和为10.
解答 解:设矩形的长和宽分别为a、b,
则a+b=7,ab=12,
所以矩形的对角线长=$\sqrt{{a}^{2}+{b}^{2}}$=$\sqrt{(a+b)^{2}-2ab}$=$\sqrt{{7}^{2}-2×12}$=5,
所以矩形的对角线之和为10.
故选D.
点评 本题考查了根与系数的关系:若x1,x2是一元二次方程ax2+bx+c=0(a≠0)的两根时,x1+x2=-$\frac{b}{a}$,x1x2=$\frac{c}{a}$.也考查了矩形的性质.

练习册系列答案
 培优三好生系列答案
培优三好生系列答案 优化作业上海科技文献出版社系列答案
优化作业上海科技文献出版社系列答案
相关题目
9.已知,菱形的周长为20,一条对角长为6,则菱形的面积( )
| A. | 48 | B. | 24 | C. | 18 | D. | 12 |
6.已知菱形的周长为40,一条对角线长为12,则这个菱形的面积为( )
| A. | 40 | B. | 47 | C. | 96 | D. | 190 |
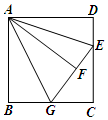 如图,在正方形ABCD中,AB=3,点E在CD边上,且CE=2DE,将△ADE沿直线AE对折至△AEF,延长EF交BC于G,连接AG,则线段AG的长为$\frac{{3\sqrt{5}}}{2}$.
如图,在正方形ABCD中,AB=3,点E在CD边上,且CE=2DE,将△ADE沿直线AE对折至△AEF,延长EF交BC于G,连接AG,则线段AG的长为$\frac{{3\sqrt{5}}}{2}$.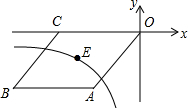 如图,O是坐标原点,菱形OABC的顶点A的坐标为(-3,-4),顶点C在x轴的负半轴上,函数y=$\frac{k}{x}$(x<0)的图象经过菱形OABC中心E点,则k的值为( )
如图,O是坐标原点,菱形OABC的顶点A的坐标为(-3,-4),顶点C在x轴的负半轴上,函数y=$\frac{k}{x}$(x<0)的图象经过菱形OABC中心E点,则k的值为( )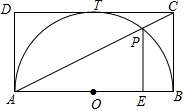 如图,在矩形ABCD中,以边AB为直径的半圆O恰与对边CD相切于T,与对角线AC交于P,PE⊥AB于E,AB=10,则PE的长为4cm.
如图,在矩形ABCD中,以边AB为直径的半圆O恰与对边CD相切于T,与对角线AC交于P,PE⊥AB于E,AB=10,则PE的长为4cm.