题目内容
9．已知，菱形的周长为20，一条对角长为6，则菱形的面积（ ）| A． | 48 | B． | 24 | C． | 18 | D． | 12 |
分析 画出图形，可得边长AB=5，由于AC⊥BD，由勾股定理可得OA及AC的值，再由菱形的面积等于两对角线的积的一半求得．
解答 解：如图，BD=6，
∵菱形的周长为20，
∴AB=5，
∵四边形ABCD是菱形，
∴OB=$\frac{1}{2}$DB=3，
由勾股定理得OA=4，则AC=8，
所以菱形的面积=$\frac{1}{2}$AC•BD=$\frac{1}{2}$×6×8=24．
故选B．
点评 本题考查了菱形的性质，需要用到菱形的对角线互相垂直且平分，及菱形的面积等于两条对角线的积的一半．
练习册系列答案
轻巧夺冠周测月考直通中考系列答案
相关题目
19．在数轴上表示不等式x＜1的解集，正确的是（ ）
| A． |  | B． |  | ||
| C． |  | D． |  |
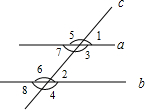如图，直线a、b都与直线c相交，给出下列条件：①∠1=∠2； ②∠3=∠6；③∠1=∠4；④∠5+∠8=180°，其中能判断a∥b的条件是：①②④．（把你认为正确的序号填在空格内）
如图所示，直线a∥b，直线c与直线a，b分别相交于点A、点B，AM⊥b，垂足为M，若∠1=50°，则∠2=40°．
如图，在直角坐标系中，△ABC的三个顶点均在格点上，其位置如图所示．现将△ABC沿AA′的方向平移，使得点A移至图中的点A′的位置，写出平移过程中线段AB扫过的面积8．
18．若矩形的长和宽是方程x2-7x+12=0的两根，则矩形的对角线之和为（ ）
| A． | 5 | B． | 7 | C． | 8 | D． | 10 |