��Ŀ����
1����ͼ��1��������ABCD�ı�AB=4��BC=8����Rt��ABC�Ƶ�B��ʱ����ת90��õ�Rt��GEF����E��B�غϣ�����GEF��B��ÿ��1����λ���ٶ�������BC���������ƶ�������G���C�غ�ʱֹͣ�˶������˶�ʱ��Ϊt�룬����������⣺��1�����˶������У���tΪ��ֵʱ��GF����A��
��2���������˶������У����GEF���ACD�ص����ֵ����ΪS����S��t�ĺ�����ϵʽ����д����Ӧ��t��ȡֵ��Χ��
��3����ͼ��2�����˶������е�0��t��8ʱ������BD��AC��O����EF���߶�BD���ڵ�P���Ƿ���ڡ�PEOΪ���������Σ������ڣ������Ӧ��t����������˵�����ɣ�

���� ��1����ͼ1������ת��ƽ�Ƶ����ʿ�֪BF=BC=E��F�䣬��F��M=ME��=4���ɵ�AMΪ��G��E��F�����λ�ߣ�����λ�ߵ����ʿɵ�AM�ij�����t��
��2�����÷������۵�˼�룬�ٵ�0��t��2ʱ����ͼ1��AM=t��MP=$\frac{1}{2}t$���ɵ�S=$\frac{1}{4}$t2��
����ͼ2����2��t��8ʱ��AN=t-2��NQ=$\frac{\sqrt{5}}{5}$��t-2�����������������ε����ʿɵ�AN=t-2��NQ=$\frac{\sqrt{5}}{5}$��t-2������S=S��MPA-S��AQN �ɵý����
�۵�8��t��10ʱ������S=S��ADC-S��ANQ������𰸣�
�ܵ�10��t��12ʱ���ɵã�CG=12-t��CM=24-2t��QC=$\frac{\sqrt{5}}{5}$��24-2t����QM=$\frac{2\sqrt{5}}{5}$��24-2t����������S=$\frac{1}{2}$QM•QC����𰸣�
��3�����ȱ�ʾ��PE2=��$\frac{1}{2}$t��2��QE2=22+��4-t��2��OP2=${��2\sqrt{5}-\frac{\sqrt{5}}{2}t��}^{2}$���ٷֱ����âٵ�PO=PEʱ���ڵ�EO=EPʱ���۵�OE=OPʱ������𰸣�
��� �⣺��1����F��M=ME��=4��
��t=AM=$\frac{1}{2}G��E��=2$��
����t=2ʱ��GF���㣻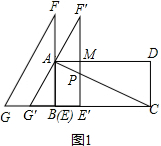
��2������ͼ1����0��t��2ʱ��AM=t��MP=$\frac{1}{2}t$��S=$\frac{1}{4}$t2��
����ͼ2����2��t��8ʱ��AN=t-2��
�ߡ�ANQ�ס�ACD��
��$\frac{NQ}{AN}$=$\frac{CD}{AC}$��
��$\frac{NQ}{t-2}$=$\frac{4}{4\sqrt{5}}$��
��NQ=$\frac{\sqrt{5}}{5}$��t-2����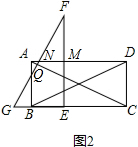
AQ=$\frac{2\sqrt{5}}{5}��t-2��$��
��S=S��MPA-S��AQN=$\frac{1}{4}$t2-$\frac{1}{2}$��$\frac{2\sqrt{5}}{5}$��$\frac{\sqrt{5}}{5}$��t-2��2
=$\frac{1}{4}$t2-$\frac{1}{5}$��t-2��2
=$\frac{1}{20}$t2+$\frac{4}{5}$t$-\frac{4}{5}$��
����ͼ3����8��t��10ʱ��
S=S��ADC-S��ANQ
=16-$\frac{1}{5}$��t-2��2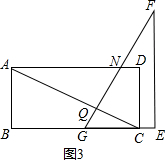
=-$\frac{1}{5}$t2+$\frac{4}{5}$t-$\frac{4}{5}$+16
=$-\frac{1}{5}$t2+$\frac{4}{5}t$$+\frac{76}{5}$��
�ܵ�10��t��12ʱ��
�ɵã�CG=12-t��CM=24-2t��QC=$\frac{\sqrt{5}}{5}$��24-2t��
QM=$\frac{2\sqrt{5}}{5}$��24-2t��
��S=$\frac{1}{2}$QM•QC
=$\frac{1}{2}��\frac{2\sqrt{5}}{5}$��$\frac{\sqrt{5}}{5}$��24-2t��2
=$\frac{1}{5}$��24-2t��2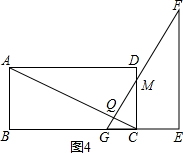
=-$\frac{4}{5}$t2-$\frac{96}{5}$t+$\frac{576}{5}$��
���ϣ���S=$\left\{\begin{array}{l}{\frac{1}{4}{t}^{2}��0��t��2��}\\{\frac{1}{20}{t}^{2}+\frac{4}{5}t-\frac{4}{5}��2��t��8��}\\{-\frac{1}{5}{t}^{2}+\frac{4}{5}t+\frac{76}{5}��8��t��10��}\\{\frac{4}{5}{t}^{2}-\frac{96}{5}t+\frac{576}{5}��10��t��12��}\end{array}\right.$��
��3����ͼ5��PE2=��$\frac{1}{2}$t��2=$\frac{1}{4}$t2��OE2=22+��4-t��2=4+16-8t+t2��
OP2=${��2\sqrt{5}-\frac{\sqrt{5}}{2}t��}^{2}$=20-10t+$\frac{5}{4}$t2��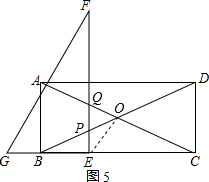
�ٵ�PO=PEʱ��
$\frac{1}{4}{t}^{2}$=20-10t+$\frac{5}{4}$t2
��ã�t=5$��\sqrt{5}$��
�ڵ�EO=EPʱ��
t2-8t+20=$\frac{1}{4}$t2��
��ã�t1=4��t2=$\frac{20}{3}$��
�۵�OE=OPʱ��
t2-8t+20=20-10t+$\frac{5}{4}$t2��
��ã�t3=0��t4=8��
��t=0ʱ��P��E�غ� ��t=4ʱ��O��P�غϣ�
����������t��ֵΪ5+$\sqrt{5}$��5-$\sqrt{5}$��$\frac{20}{3}$��8��
���� ������Ҫ�������ı����ۺ��Լ����ɶ��������������ε��ж������ʡ����������ε����ʵ�֪ʶ����ȷ���÷������۵ó�t��ֵ�Լ���Ϸֶκ������������ϵʽ�ǽ���ؼ���

| A�� | 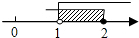 | B�� | 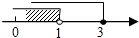 | C�� | 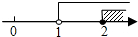 | D�� |  |
| A�� | 2 | B�� | 3 | C�� | 4 | D�� | 12 |
| A�� | -3ab2 | B�� | -3ab | C�� | 3ab | D�� | 3ab2 |
| A�� | 1 | B�� | 2 | C�� | 3 | D�� | 4 |